Question

【题目】在平面直角坐标系内，直线l⊥y轴于点C(C在y轴的正半轴上)，与直线y=相交于点A，和双曲线y=交于点B，且AB=6，则点B的坐标是______．

Answer 1

【答案】（3+，）或（-3+，）

【解析】

根据直线l⊥y轴，可知AB∥x轴，则A、B的纵坐标相等，设A（m，m）（m＞0），列方程 ，可得点B的坐标，根据AB=6，列关于m的方程可得结论．

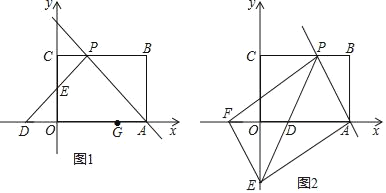
如图，

设A（m，m）（m＞0），如图所示，

∴点B的纵坐标为m，

∵点B在双曲线y＝上，

∴，

∴x=，

∵AB=6，

即|m-|=6，

∴m-=6或-m=6，

∴m1=3+或m2=3-＜0（舍），m3=-3-（舍），m4=-3+，

∴B（3+，）或（-3+，），

故答案为：（3+，）或（-3+，）．