题目内容
抛物线y＝x＋4x＋5是由抛物线y＝x＋1经过某种平移得到，则这个平移可以表述为( )
| A．向上平移2个单位 | B．向左平移2个单位 |
| C．向下平移4个单位 | D．向右平移2个单位 |
B.
解析试题分析：找到两个抛物线的顶点，根据抛物线的顶点即可判断是如何平移得到．
原抛物线的顶点为（0，1），新抛物线的顶点为（-2，1），
∴是抛物线y=x2+1向左平移2个单位得到，
故选B．
考点: 二次函数图象与几何变换．
练习册系列答案
相关题目
甲、乙两位同学对问题“求代数式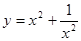
的最小值”提出各自的想法．甲说：“可以利用已经学过的完全平方公式，把它配方成
，所以代数式的最小值为-2”．乙说：“我也用配方法，但我配成
，最小值为2”．你认为（ ）
| A．甲对 | B．乙对 | C．甲、乙都对 | D．甲乙都不对 |
如图，抛物线y=ax2+bx+c与x轴的负半轴交于点A，B（点A在点B的右边），与y轴的正半轴交于点C，且OA=OC=1，则下列关系中正确的是（ ）
| A．a+b=1 | B．b<2a | C．a-b=-1 | D．ac<0 |
二次函数y=kx2﹣6x+3的图象与x轴有交点，则k的取值范围是（ ）
| A．k＜3 | B．k＜3且k≠0 |
| C．k≤3 | D．k≤3且k≠0 |
A
，B
，C
是抛物线
上三点，
的大小关系为（ ）
A． | B． | C． | D． |
抛物线y=3x2，y=-3x2，y=
x2+3共有的性质是
| A．开口向上 | B．对称轴是y轴 |
| C．都有最高点 | D．y随x值的增大而增大 |
下列关于抛物线
和
的关系说法中，正确的是（ ）
| A．它们的形状相同，开口也相同； |
B．它们都关于 轴对称； |
| C．它们的顶点不相同； |
D．点（ ， ）既在抛物线上也在上 |