ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ ![]() ЪЧе§ЗНаЮЃЌ
ЪЧе§ЗНаЮЃЌ ![]() ЪЧ
ЪЧ ![]() ДЙжБЦНЗжЯпЩЯЕФЕуЃЌЕу
ДЙжБЦНЗжЯпЩЯЕФЕуЃЌЕу ![]() Йигк
Йигк ![]() ЕФЖдГЦЕуЪЧ
ЕФЖдГЦЕуЪЧ ![]() ЃЌжБЯп
ЃЌжБЯп ![]() гыжБЯп
гыжБЯп ![]() НЛгкЕу
НЛгкЕу ![]() .
.
ЃЈ1ЃЉШєЕу ![]() ЪЧ
ЪЧ ![]() БпЕФжаЕуЃЌСЌНг
БпЕФжаЕуЃЌСЌНг ![]() ЃЌдђ
ЃЌдђ ![]() ЃНЃЛ
ЃНЃЛ
ЃЈ2ЃЉаЁУїДгРЯЪІФЧРяСЫНтЕНЃЌжЛвЊЕу ![]() ВЛдке§ЗНаЮЕФжааФЃЌдђжБЯп
ВЛдке§ЗНаЮЕФжааФЃЌдђжБЯп ![]() гы
гы ![]() ЫљМаШёНЧВЛБфЃЎЫћГЂЪдИФБфЕу
ЫљМаШёНЧВЛБфЃЎЫћГЂЪдИФБфЕу ![]() ЕФЮЛжУЃЌМЦЫуЯргІНЧЖШЃЌбщжЄРЯЪІЕФЫЕЗЈЃЎ
ЕФЮЛжУЃЌМЦЫуЯргІНЧЖШЃЌбщжЄРЯЪІЕФЫЕЗЈЃЎ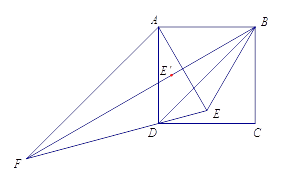
ШчЭМЃЌНЋЕу ![]() бЁдке§ЗНаЮФкЃЌЧвЁї
бЁдке§ЗНаЮФкЃЌЧвЁї ![]() ЮЊЕШБпШ§НЧаЮЃЌЧѓГіжБЯп
ЮЊЕШБпШ§НЧаЮЃЌЧѓГіжБЯп ![]() гы
гы ![]() ЫљМаШёНЧЕФЖШЪ§ЃЛ
ЫљМаШёНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЧыФуМЬајбаОПетИіЮЪЬтЃЌПЩвдбгајаЁУїЕФЯыЗЈЃЌвВПЩгУЦфЫќЗНЗЈ.
ЮвбЁдёаЁУїЕФЯыЗЈЃЛВЂМђЪіЧѓжБЯп ![]() гы
гы ![]() ЫљМаШёНЧЖШЪ§ЕФЫМТЗЃЎ
ЫљМаШёНЧЖШЪ§ЕФЫМТЗЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ45
ЃЈ2ЃЉ
НтЃКЁп ![]() ЪЧЕШБпШ§НЧаЮЃЌ
ЪЧЕШБпШ§НЧаЮЃЌ
Ёр ![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
ЁпЫФБпаЮ ![]() ЪЧе§ЗНаЮЃЌ
ЪЧе§ЗНаЮЃЌ
Ёр ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
Ёр ![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
Ёр ![]() ЃЎ
ЃЎ
ЁпЕу ![]() ЪЧЕу
ЪЧЕу ![]() Йигк
Йигк ![]() ЕФЖдГЦЕуЃЌ
ЕФЖдГЦЕуЃЌ
Ёр ![]() ЃЎ
ЃЎ
Ёр ![]() ЃЎ
ЃЎ
Ёр ![]() ЃЎ
ЃЎ
Ёр ![]() ЃЎ
ЃЎ
Ёп ![]() ЃЌ
ЃЌ
Ёр ![]() Ёе
Ёе ![]()
Ёр ![]() ЃЎ
ЃЎ
Ёр ![]() ЃЎ
ЃЎ
Ёр ![]()
ЃЈ3ЃЉ
НтЃКШчЙћбигУаЁУїЕФЯыЗЈЃК
ЗНЗЈвЛЃКШчЭМЃЌЮвНЋЕу ![]() бЁдк
бЁдк ![]() БпЕФжаЕуЃЎ
БпЕФжаЕуЃЎ
ЁпЫФБпаЮ ![]() ЪЧе§ЗНаЮЃЌ
ЪЧе§ЗНаЮЃЌ
Ёр ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
ЁпЕу ![]() ЪЧЕу
ЪЧЕу ![]() Йигк
Йигк ![]() ЕФЖдГЦЕуЃЌ
ЕФЖдГЦЕуЃЌ
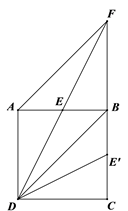
Ёр ![]() .
.
Ёр ![]() .
.
Ёр ![]() дк
дк ![]() ЩЯ.
ЩЯ.
Ёр ![]() дкжБЯп
дкжБЯп ![]() ЩЯ.
ЩЯ.
Ёр ![]() .
.
Ёр ![]() ЃЌ
ЃЌ ![]() .
.
Ёп ![]() ЪЧ
ЪЧ ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
Ёр ![]() ЃЌ
ЃЌ
Ёр ![]() Ёе
Ёе ![]() ЃЎ
ЃЎ
Ёр ![]() .
.
Ёр ![]() .
.
Ёп ![]() ЃЌ
ЃЌ
Ёр ![]() ЪЧЕШбќжБНЧШ§НЧаЮ.
ЪЧЕШбќжБНЧШ§НЧаЮ.
Ёр ![]() .
.
Ёр ![]() .
.
ЁржБЯп ![]() гы
гы ![]() ЫљМаШёНЧЮЊ
ЫљМаШёНЧЮЊ ![]() ЃЎ
ЃЎ
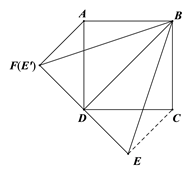
ЗНЗЈЖўЃКШчЭМЃЌЮвНЋЕу ![]() бЁдке§ЗНаЮЭтЃЌЪЙ
бЁдке§ЗНаЮЭтЃЌЪЙ ![]() ЕФЮЛжУЃЌ
ЕФЮЛжУЃЌ
СЌНг ![]() ЃЎ
ЃЎ
ЁпЫФБпаЮ ![]() ЪЧе§ЗНаЮЃЌ
ЪЧе§ЗНаЮЃЌ
Ёр ![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
Ёп ![]() дк
дк ![]() ЕФДЙжБЦНЗжЯпЩЯЃЌ
ЕФДЙжБЦНЗжЯпЩЯЃЌ
Ёр ![]() ЃЎ
ЃЎ
Ёр ![]() ЃЎ
ЃЎ
Ёп ![]() ЃЌ
ЃЌ
Ёр ![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
Ёр ![]() ЃЎ
ЃЎ
ЁпЕу ![]() ЪЧЕу
ЪЧЕу ![]() Йигк
Йигк ![]() ЕФЖдГЦЕуЃЌ
ЕФЖдГЦЕуЃЌ
Ёр ![]() ЃЎ
ЃЎ
Ёр ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() Ш§ЕуЙВЯп.
Ш§ЕуЙВЯп.
ЁрЕу ![]() гыЕу
гыЕу ![]() жиКЯЃЎ
жиКЯЃЎ
Ёр ![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
Ёр ![]() ЃЎ
ЃЎ
Ёр ![]() Ёе
Ёе ![]() ЃЎ
ЃЎ
Ёр ![]() ЃЎ
ЃЎ
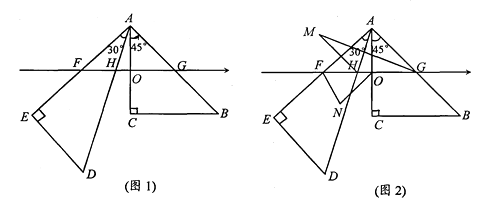
ЁОНтЮіЁПЃЈ1ЃЉИљОнвбжЊЬѕМўЛГіЭМаЮМДПЩЧѓЕУЁЯ FADЖШЪ§.
ЃЈ2ЃЉгЩЕШБпШ§НЧаЮЕФаджЪЕУ ЁЯEBA=ЁЯEAB=60Ёу ЃЌ BE=EA=AB ЃЛгЩе§ЗНаЮаджЪЕУ AB=AD ЃЌ ЁЯABD=45Ёу ЃЌ ЁЯBAD=90Ёу ЃЛЕШСПДњЛЛЕУAE=ADЃЌ ЃЛ ЁЯEAD=ЁЯBADЁЯBAE=30Ёу ЃЌ ЁЯAED=75Ёу ЃЛгЩЬѕМўжЄІЄABF Ёе ІЄEBFЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУFA=FE ЃЛЁЯFAE=ЁЯFEA=75Ёу ЃЛЁЯFAD=ЁЯFAEЁЯEAD=45Ёу
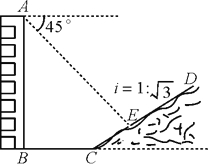
ЃЈ3ЃЉЕу E бЁдке§ЗНаЮЭтЃЌЪЙ ЁЯEDC=45Ёу ЕФЮЛжУЃЌСЌНг CE ЃЎ
гЩе§ЗНаЮаджЪЕУЃЌ DA=DC ЃЌ ЁЯBDA=ЁЯBDC=45Ёу ЃЛгЩEДЙжБЦНЗжЯпЕУаджЪЕУED=CE ЃЌгЩЕШбќШ§НЧаЮЕФаджЪЕУEDЁЭBD ЃЛдйгЩвбжЊЬѕМўжЄ
ІЄADF Ёе ІЄCDE ЃЛИљОнЕШбќШ§НЧаЮЕФаджЪЕУ ЁЯFAD=ЁЯECD=45Ёу .
ЁОПМЕуОЋЮіЁПеЦЮеЕШбќжБНЧШ§НЧаЮКЭЕШБпШ§НЧаЮЕФаджЪЪЧНтД№БОЬтЕФИљБОЃЌашвЊжЊЕРЕШбќжБНЧШ§НЧаЮЪЧСНЬѕжБНЧБпЯрЕШЕФжБНЧШ§НЧаЮЃЛЕШбќжБНЧШ§НЧаЮЕФСНИіЕзНЧЯрЕШЧвЕШгк45ЁуЃЛЕШБпШ§НЧаЮЕФШ§ИіНЧЖМЯрЕШВЂЧвУПИіНЧЖМЪЧ60ЁуЃЎ