题目内容
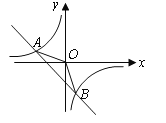
【题目】如图，已 知直线
交坐标轴于
两点，以线段
为边向上作正方形
，过点
的抛物线与直线另一个交点为
．
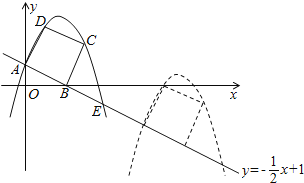
（1）请直接写出点
的坐标；
（2）求抛物线的解析式；
（3）若正方形以每秒
个单位长度的速度沿射线下滑，直至顶点
落在x轴上时停止．设正方形落在
轴下方部分的面积为
，求关于滑行时间
的函数关系式，并写出相应自变量的取值范围；
（4）在（3）的条件下，抛物线与正方形一起平移，同时停止，求抛物线上
两点间的抛物线弧所扫过的面积．
【答案】（1）C（3，2）D（1，3）；
（2）y=-
x2+
x+1
（3）当0<t≤1时，S△FB′G=
FB′×GB′=
t
=
t2
当1<t≤2时，S梯形A′B′HG =
t-；
2<t≤3时，S五边形GA′B′C′H=-t2+
t-
（4）15.
【解析】
（1）可先根据AB所在直线的解析式求出A，B两点的坐标，即可得出OA、OB的长．过D作DM⊥y轴于M，则△ADM≌△BAO，由此可得出MD、MA的长，也就能求出D的坐标，同理可求出C的坐标；
（2）可根据A、C、D三点的坐标，用待定系数法求出抛物线的解析式；
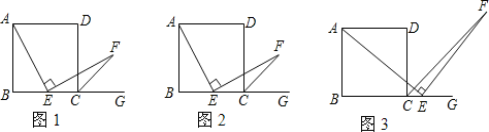
（3）要分三种情况进行讨论：
①当F点在A′B′之间时，即当0<t≤1时，此时S为三角形FBG的面积，可用正方形的速度求出AB′的长，即可求出B′F的长，然后根据∠GFB′的正切值求出B′G的长，即可得出关于S、t的函数关系式．
②当A′在x轴下方，但C′在x轴上方或x轴上时，即当1<t≤2时，S为梯形A′GB′H的面积，可参照①的方法求出A′G和B′H的长，那么梯形的上下底就可求出，梯形的高为A′B′即正方形的边长，可根据梯形的面积计算公式得出关于S、t的函数关系式．
③当D′逐渐移动到x轴的过程中，即当2<t≤3时，此时S为五边形A′B′C′HG的面积，S=正方形A′B′C′D′的面积-三角形GHD′的面积．可据此来列关于S，t的函数关系式；
（4）CE扫过的图形是个平行四边形，经过关系不难发现这个平行四边形的面积实际上就是矩形BCD′A′的面积．可通过求矩形的面积来求出CE扫过的面积．
（1）C（3，2）D（1，3）；
（2）设抛物线为y=ax2+bx+c，抛物线过（0，1）（3，2）（1，3），
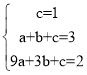
解得
y=-x2+x+1
（3）①当点A运动到x轴上时，t=1，
当0<t≤1时，如图1，
∵∠OFA=∠GFB′，
tan∠OFA=
=
∴tan∠GFB′=
=
=
∴GB′=
∴S△FB′G=FB′×GB′=t=t2
②当点C运动到x轴上时，t=2，
当1<t≤2时，如图2，
A′B′=AB=
=
，
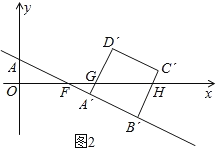
∴A′G=
∵B′H=
∴S梯形A′B′HG=（A′G+B′H）×A′B′= (+)×=t-；
③当点D运动到x轴上时，t=3，
当2<t≤3时，如图3，
∵A′G=
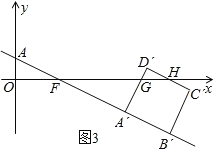
∴GD′=-=
，
∵S△AOF=×1×2=1，OA=1，△AOF∽△GD′H
∴
=（
）2
∴S△GD′H=()2，
∴S五边形GA′B′C′H=（）2-（)2=-t2+t-；
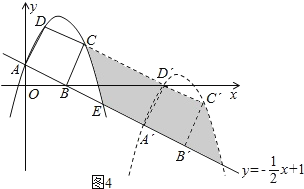
（4）∵t=3，BB′=AA′=3，
∴S阴影=S矩形BB′C′C=S矩形AA′D′D
=AD×AA′=×3=15．
