题目内容
如图,将![]() 置于平面直角坐标系中,其中点
置于平面直角坐标系中,其中点![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,
,![]() .
.

(1)若![]() 的外接圆与
的外接圆与![]() 轴交于点
轴交于点![]() ,求
,求![]() 点坐标.
点坐标.
(2)若点![]() 的坐标为
的坐标为![]() ,试猜想过
,试猜想过![]() 的直线与
的直线与![]() 的外接圆的位置关系,并加以说明.
的外接圆的位置关系,并加以说明.
(3)二次函数的图象经过点![]() 和
和![]() 且顶点在圆上,求此函数的解析式.
且顶点在圆上,求此函数的解析式.
解:(1)连结AD,则∠ADO=∠B=600
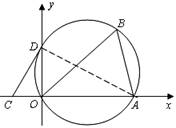
在Rt△ADO中,∠ADO=600
所以OD=OA÷![]() =3÷
=3÷![]() =
=![]()
所以D点的坐标是(0,![]() )
)
(2)猜想是CD与圆相切
∵ ∠AOD是直角,所以AD是圆的直径
又∵ Tan∠CDO=CO/OD=1/![]() =
=![]() , ∠CDO=300
, ∠CDO=300
∴∠CDA=∠CDO+∠ADO=Rt∠ 即CD⊥AD
∴ CD切外接圆于点D
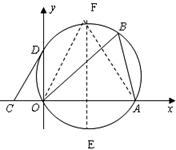
(3)依题意可设二次函数的解析式为 :
y=α(x-0)(x-3)
由此得顶点坐标的横坐标为:x=![]() =
=![]() ;
;
即顶点在OA的垂直平分线上,作OA的垂直平分线EF,则得∠EFA=![]() ∠B=300
∠B=300
得到EF=![]() EA=
EA=![]()
可得一个顶点坐标为(![]() ,
,![]() )
)
同理可得另一个顶点坐标为(![]() ,
,![]() )
)
分别将两顶点代入y=α(x-0)(x-3)可解得α的值分别为![]() ,
,![]()
则得到二次函数的解析式是y=![]() x(x-3)或y=
x(x-3)或y=![]() x(x-3)
x(x-3)

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 (2)若点
(2)若点 其中点
其中点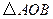 置于平面直角坐标系中,
置于平面直角坐标系中, 其中点
其中点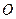 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为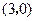 ,
,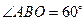 .
.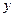 轴交于点
轴交于点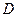 ,求
,求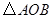 置于平面直角坐标系中,
置于平面直角坐标系中, 其中点
其中点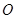 为坐标原点,点
为坐标原点,点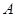 的坐标为
的坐标为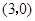 ,
,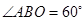 .
.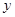 轴交于点
轴交于点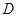 ,求
,求