Question

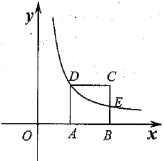
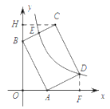
【题目】如图，矩形的边，点，分别在轴，轴上，反比例函数的图象经过点，且与边交于点.

（1）求反比例函数的解析式；

（2）求点的坐标.

Answer 1

【答案】(1) ；(2)点的坐标为（2，7）．

【解析】

（1）首先过点D作DF⊥x轴于点F，易证得△AOB∽△DFA，然后由相似三角形的对应边成比例，求得点D的坐标，即可求得反比例函数的解析式，

（2）利用平移的性质求得点C的坐标，继而求得直线BC的解析式，则可求得点E的坐标．

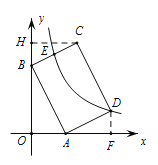
（1）过点作轴于点，

则，∴，

∵四边形是矩形，

∴，∴，∴，

∴，

∴，

∵，，，∴，，

∴，∴点的坐标为：（7，2），

∴反比例函数的解析式为：

(2)过点作轴于点，则,,

∴点的坐标为：（4，8），

设直线的解析式为：，则，解得：，∴直线的解析式为：，

得得：或（舍去），∴点的坐标为：（2，7）．