题目内容
 四边形ABCD中,∠ABC=135°,∠BCD=120°,AB=
四边形ABCD中,∠ABC=135°,∠BCD=120°,AB= ,BC=
,BC= ,CD=6,则AD=________.
,CD=6,则AD=________.

分析:作AE⊥BC,DE⊥BC,AG⊥DF,则四边形AEFG为矩形,AE=FG.EF=AG,因为△ADG为直角三角形,所以AD=
 ,根据直角△AEB和直角△CDF即可求AE,BE,CF,FD.
,根据直角△AEB和直角△CDF即可求AE,BE,CF,FD.解答:
 解:作AE⊥BC,DF⊥BC,AG⊥DF,
解:作AE⊥BC,DF⊥BC,AG⊥DF,则四边形AEFG四个内角均为直角,
∴四边形AEFG为矩形,AE=FG.EF=AG
∠ABE=180°-135°=45°,∠DCF=180°-120°=60°,
∴AE=EB=
 ×
× =
= ,CF=
,CF= ×CD=3,FD=
×CD=3,FD= CF=3
CF=3 ,
,∴AG=EF=8,DG=DF-AE=2
 ,
,∴AD=
 =
= ,
,故答案为
 .
.点评:本题考查了矩形的判定和矩形对边相等的性质,考查了勾股定理在直角三角形中的运用,本题中构造矩形AEFG是解题的关键.

练习册系列答案
相关题目
 23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.
23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.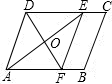 如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )
如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( ) 17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形:
17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形: 7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.
7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.