题目内容
如图，△ABC的面积等于1，在图2中，| AD |
| AB |
| BE |
| BC |
| CF |
| CA |
| 1 |
| 2 |
| AD |
| AB |
| BE |
| BC |
| CF |
| CA |
| 1 |
| 3 |
| AD |
| AB |
| BE |
| BC |
| CF |
| CA |
| 1 |
| 4 |
| AD |
| AB |
| BE |
| BC |
| CF |
| CA |
| 1 |
| n |
| 3 |
| 5 |
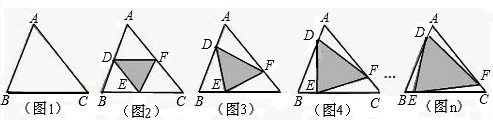
分析：设S△ADF=S1，S△BDE=S2，S△CFE=S3，S△DEF=S，AB=c，BC=a，AC=b．根据
=
=
=
，可以求得△ADF，△BDE，△CEF的两个边长与a，b，c的关系，再根据三角形的面积公式S=
absinc求得△DEF的面积公式S=2-3×
，最后根据题意解不等式即可．
| AD |
| AB |
| BE |
| BC |
| CF |
| CA |
| 1 |
| n |
| 1 |
| 2 |
| n-1 |
| n2 |
解答：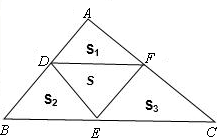
解：
根据题意，画出上图，
设S△ADF=S1，S△BDE=S2，S△CFE=S3，S△DEF=S，AB=c，BC=a，AC=b，
∵S△ABC=
acsinB=
bcsinA=
absinC①
∵△ABC的面积等于1，
∴由①得，sinA=
，sinB=
，sinC=
，
∵
=
=
=
，
∴AD=
，BE=
，CF=
，
∴BD=c（1-
），EC=a（1-
），AF=b（1-
），
∴S1=S2=S3=
，
∴S=1-S1-S2-S3=2-3×
∵△DEF的面积小于
，
∴1-3×
＜
，2n2-15n+15＜0（n≥2且是自然数），解得2≤n≤6．
∴从图2到图n中，共有5张图，△DEF的面积小于
．
解：根据题意，画出上图，
设S△ADF=S1，S△BDE=S2，S△CFE=S3，S△DEF=S，AB=c，BC=a，AC=b，
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC的面积等于1，
∴由①得，sinA=
| 2 |
| bc |
| 2 |
| ac |
| 2 |
| ab |
∵
| AD |
| AB |
| BE |
| BC |
| CF |
| CA |
| 1 |
| n |
∴AD=
| c |
| n |
| a |
| n |
| b |
| n |
∴BD=c（1-
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
∴S1=S2=S3=
| n-1 |
| n2 |
∴S=1-S1-S2-S3=2-3×
| n-1 |
| n2 |
∵△DEF的面积小于
| 3 |
| 5 |
∴1-3×
| n-1 |
| n2 |
| 3 |
| 5 |
∴从图2到图n中，共有5张图，△DEF的面积小于
| 3 |
| 5 |
点评：本题主要考查的是三角形的面积公式S=
absinc．
| 1 |
| 2 |
练习册系列答案
相关题目
如图，△ABC的面积是63，D是BC上的一点，且BD：CD=2：1，DE∥AC交AB于E，延长DE到F，使FE：ED=2：1，则△CDF的面积是
如图，△ABC的面积为1，分别取AC、BC两边的中点A1、B1，则四边形A1ABB1的面积为
如图，△ABC的面积为
3、如图，△ABC的面积为1，若把△ABC的各边分别延长一倍，得到一个新的△DEF，则S△DEF=
如图，△ABC的面积为1．第一次操作：分别延长AB，BC，CA至点A1，B1，C1，使A1B=AB，B1C=BC，C1A=CA，顺次连结A1，B1，C1，得到△A1B1C1．第二次操作：分别延长A1B1，B1C1，C1A1至点A2，B2，C2，使A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连结A2，B2，C2，得到△A2B2C2．…按此规律，要使得到的三角形的面积超过2013，最少经过