题目内容
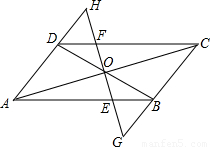
过?ABCD对角线AC、BD的交点O作一条直线，分别交AB和DC于E、F两点，交CB和AD的延长线于G、H两点．求证：OG=OH．
证明：∵四边形ABCD是平行四边形，
∴OB=OD．
∵AD∥BC，∴∠H=∠G．
在△DOH与△OBG中，
∠DOH=∠BOG，∠H=∠G，OD=OB，
∴△ODH≌△OBG，
∴OH=OG．
分析：由题中条件及平行四边形的性质不难得出△ODH≌△OBG，进而可得出结论．
点评：本题主要考查平行四边形的性质及全等三角形的判定及性质，能够熟练掌握．
∴OB=OD．
∵AD∥BC，∴∠H=∠G．
在△DOH与△OBG中，
∠DOH=∠BOG，∠H=∠G，OD=OB，
∴△ODH≌△OBG，
∴OH=OG．
分析：由题中条件及平行四边形的性质不难得出△ODH≌△OBG，进而可得出结论．
点评：本题主要考查平行四边形的性质及全等三角形的判定及性质，能够熟练掌握．
练习册系列答案
计算高手系列答案
相关题目
7、如图所示，EF过?ABCD对角线的交点O，分别交AD于E，交BC于点F，若OE=5，四边形CDEF的周长为25，则?ABCD的周长为（ ）
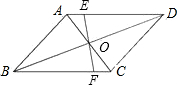如图，EF过?ABCD对角线的交点O，并交AD于E，交BC于F，若AB=4，BC=5，OE=1.5，则四边形EFCD的周长是（ ）| A、16 | B、14 | C、12 | D、10 |
22、过?ABCD对角线AC、BD的交点O作一条直线，分别交AB和DC于E、F两点，交CB和AD的延长线于G、H两点．求证：OG=OH．