题目内容
解方程组: .
.
解: ,
,
由①可设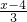 =
= =
= =k,
=k,
x=3k+4,y=4k-1,z=5k-2,
代入方程②得,3k+4-2(4k-1)+3(5k-2)=30,
去括号得,3k+4-8k+2+15k-6=30,
解得k=3,
所以x=3×3+4=13,
y=4×3-1=11,
z=5×3-2=13,
因此,这个方程组的解是 .
.
分析:设第一个方程的值为k,表示出x、y、z,然后代入第二个方程求出k值,从而得解.
点评:本题考查了解三元一次方程组,解三元一次方程组主要思想是消元,本题根据第一个方程利用k表示出x、y、z是解题的关键.
 ,
,由①可设
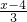 =
= =
= =k,
=k,x=3k+4,y=4k-1,z=5k-2,
代入方程②得,3k+4-2(4k-1)+3(5k-2)=30,
去括号得,3k+4-8k+2+15k-6=30,
解得k=3,
所以x=3×3+4=13,
y=4×3-1=11,
z=5×3-2=13,
因此,这个方程组的解是
 .
.分析:设第一个方程的值为k,表示出x、y、z,然后代入第二个方程求出k值,从而得解.
点评:本题考查了解三元一次方程组,解三元一次方程组主要思想是消元,本题根据第一个方程利用k表示出x、y、z是解题的关键.

练习册系列答案
相关题目
 (1)解方程组:
(1)解方程组: