Question

如图，正方形ABCD的边长是3，点P是直线BC上一点，连接PA，将线段PA绕点P逆时针旋转得到线段PE，在直线BA上取点F，使BF=BP，且点F与点E在BC同侧，连接EF，CF.

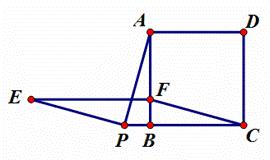
⑴如图，当点P在CB延长线上时，求证：四边形PCFE是平行四边形；

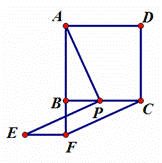
⑵如图‚，当点P在线段BC上时，四边形PCFE是否还是平行四边形，说明理由；

⑶在⑵的条件下，四边形PCFE的面积是否有最大值？若有，请求出面积的最大值及此时BP长；若没有，请说明理由。

第25题  图

第25题  图‚

Answer 1

（1）证法一：如图①

∵四边形ABCD是正方形，

∴AB=BC,∠ABC=∠PBA=90°

又∵BP=BF   

∴△PBA≌△FBC                ……………1分

∴PA=FC  ∠PAB=∠FCB   

又∵PA=PE     ∴PE=FC         ……………2分

∵∠PAB+∠APB= 90°      ∴∠FCB+∠APB= 90°                                

又∵∠EPA=90°

∴∠APB+∠EPA+∠FPC=180°

即∠EPC+∠PCF=180°         

∴EP∥FC                    ………………4分

∴四边形EPCF是平行四边形.  ………………5分

证法二：延长CF与AP相交于点G，如图②             

∵四边形ABCD是正方形，

∴AB=BC,     ∠ABC=∠PBA=90°       

又∵BP=BF   

∴△PBA≌△FCB                        ……………1分 第26题 图②

       ∴∠PAB=∠FCB,AP=CF

又∵PA=PE     ∴PE=FC                ……………2分

       ∵∠PAB+∠APB=90°∴∠FCB+∠APB=90°

       ∴∠PGC=90°∴∠PGC=∠APE=90°∴EP∥FC      ……4分

∴四边形EPCF是平行四边形.                ………5分

（2）证法一：结论：四边形EPCF是平行四边形，如图③ ……6分           

∵四边形ABCD是正方形，

∴AB=BC,     ∠ABC=∠CBF=90°    

又∵BP=BF    ∴△PBA≌△FBC           ……………7分

∴PA=FC   ∠PAB=∠FCB                                      

又∵PA=PE     ∴PE=FC                 ……………8分

∵∠FCB+∠BFC= 90°

∠EPB+∠APB= 90°                                           第25题图③

∴∠BPE=∠FCB             

∴EP∥FC                           ………………9分

∴四边形EPCF是平行四边形.         ………………10分

证法二：结论：四边形EPCF是平行四边形   ……………6分

延长AP与FC相交于点G如图④         

∵四边形ABCD是正方形，

∴AB=BC,     ∠ABC=∠CBF=90°    

又∵BP=BF    ∴△PBA≌△FBC           ……………7分        

∴PA=FC   ∠PAB=∠FCB                   

 又∵PA=PE     ∴PE=FC                 ……………8分

∵∠FCB+∠BFC=90°

∴∠PAB+∠BFC=90°

∴∠PGF=90°

∴∠PGF=∠APE=90°

∴EP∥FC                            ………………9分        第25题④图

∴四边形EPCF是平行四边形.          ………………10分

(3)解：设BP=x，则PC=3-x  平行四边形PEFC的面积为S,    …………………11分          

 S=PC·BF=PC·PB=  ……………12分 

        当时, =   …………………………………………………13分

∴当BP=时，四边形PCFE的面积最大，最大值为. …………………14分