Question

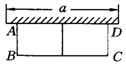
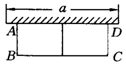
如图26-3-15所示，有长为24m的篱笆，一面利用墙（墙的最大可用长度a为10m），围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为xm，面积为Sm．

    （1）求S与x的函数关系式；

    （2）如果要围成面积为45m²的花圃，AB的长是多少？

    （3）能围成面积比45m²更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由．

Answer 1

（1）∵AB=xm，

    ∴BC=（24-3x）m．

    ∴S=x（24-3x）=-3x²+24x．

    ∵x>0，0<24-3x≤10，

    ∴≤x<8．

    ∴S与x的函数关系式是S=-3x²+24x（≤x<8）．

    （2）当S=45时，-3x²+24x=45，即x²-8x+15=0．

    解得x₁=3，x₂=5．

    而当x=3时，不满足≤x<8，故舍去，只取x=5．

    ∴要围成面积为45m²的花圃，AB的长是5m．

    （3）不能围成面积比45m²更大的花圃．

    ∵当S>45时，-3x²+24x>45，即x²-8x+15>0．

    ∴（x-3）（x-5）>0．

    ∵≤x<8，∴x-3>0，x-5>0．    ∴x>5，∴5<x<8．    ∵S=-3x²+24x=-3（x-4）²+48，

    ∴当x>4时，S随x的增大而减小．

    ∴当5<x<8时，S随x的增大而减小．∴不能围成面积比45m²更大的花辅．