题目内容
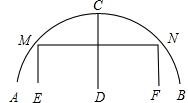 有一座圆弧形的拱桥,桥下水面宽度8m,拱顶高出水面2m.现有一货船载一货箱欲从桥下经过,已知货箱宽6m,高1.5m(货箱底与水面持平),问该货船能否顺利通过该桥?
有一座圆弧形的拱桥,桥下水面宽度8m,拱顶高出水面2m.现有一货船载一货箱欲从桥下经过,已知货箱宽6m,高1.5m(货箱底与水面持平),问该货船能否顺利通过该桥?
分析:作出弧AB所在圆的圆心O,连接OA、ON,设OA=r,先由垂径定理得出MH=NH,再用勾股定理求出r的值,在Rt△ONH中利用勾股定理求出FN的长即可作出判断.
解答: 解:作出弧AB所在圆的圆心O,连接OA、ON,
解:作出弧AB所在圆的圆心O,连接OA、ON,
则NH=
MN=
×6=3,
设OA=r,则OD=OC-CD=r-2,AD=
AB=4,
在Rt△AOD中,
∵OA2=AD2+OD2,
∴r2=42+(r-2)2,
∴r=5(m)
在Rt△ONH中,OH2=ON2-NH2
∴OH=
=4(m),
∴FN=DH=OH-OD=4-3=1(m),
∵1<1.5,
∴货船不可以顺利通过这座拱桥.
 解:作出弧AB所在圆的圆心O,连接OA、ON,
解:作出弧AB所在圆的圆心O,连接OA、ON,则NH=
| 1 |
| 2 |
| 1 |
| 2 |
设OA=r,则OD=OC-CD=r-2,AD=
| 1 |
| 2 |
在Rt△AOD中,
∵OA2=AD2+OD2,
∴r2=42+(r-2)2,
∴r=5(m)
在Rt△ONH中,OH2=ON2-NH2
∴OH=
| 52-32 |
∴FN=DH=OH-OD=4-3=1(m),
∵1<1.5,
∴货船不可以顺利通过这座拱桥.
点评:本题考查的是垂径定理及勾股定理在实际生活中的运用,根据题意作出辅助线构造出直角三角形是解答此题的关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图所示,某地有一座圆弧形的拱桥,桥下水面宽为12米,拱顶高出水面4米.
如图所示,某地有一座圆弧形的拱桥,桥下水面宽为12米,拱顶高出水面4米.