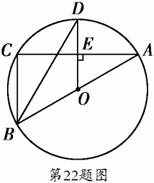
题目内容
如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，连接BD.
(1)求证：BD平分∠ABC；
(2) 当∠ODB=30°时，求证：BC=OD.
证明： （1） ∵OD⊥AC OD为半径∴
∴∠CBD=∠ABD ∴BD平分∠ABC
（2） ∵OB=OD∴∠OBD=∠ODB=30°∴∠AOD=∠OBD+∠ODB=30°+30°=60°
又∵OD⊥AC于E ∴∠OEA=90°∴∠A=180°-∠OEA-∠AOD=180°-90°-60°=30°
又∵AB为⊙O的直径 ∴∠ACB＝90°则在Rt△ACB中BC=
AB ∵OD=AB ∴BC=OD
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
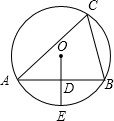如图，⊙O是△ABC的外接圆，OD⊥AB于点D、交⊙O于点E，∠C=60°，如果⊙O的半径为2，那么OD=
24、如图，AD是△ABC的高，且AD平分∠BAC，请指出∠B与∠C的关系，并说明理由．
（2013•雅安）如图，DE是△ABC的中位线，延长DE至F使EF=DE，连接CF，则S△CEF：S四边形BCED的值为（ ）
（2012•黔东南州）如图，⊙O是△ABC的外接圆，圆心O在AB上，过点B作⊙O的切线交AC的延长线于点D．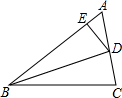
如图，BD是∠ABC的平分线，DE⊥AB于E，S△ABC=90，AB=18，BC=12，求DE的长．