题目内容
 (2013•怀柔区二模)如图,等边△ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点.设线段MN运动的时间为t秒,四边形MNQP的面积为S厘米2.则表示S与t的函数关系的图象大致是( )
(2013•怀柔区二模)如图,等边△ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点.设线段MN运动的时间为t秒,四边形MNQP的面积为S厘米2.则表示S与t的函数关系的图象大致是( )分析:过点C作CD⊥AB于D,根据等边三角形的性质可得AD=BD=
AB,然后分:①点N在AD上时,P、Q都在AC上,利用∠A的正切值表示出PM、QN,然后根据梯形的面积公式列式整理即可得到S与t的函数关系式;②点N在BD上,点M在AD上时,点P在在AC上,点Q在BC上,先表示出AM、BN,再利用∠A、∠B的正切值表示出PM、QN,然后根据梯形的面积公式列式整理即可得到S与t的函数关系式;③点M在BD上时,点P、Q都在BC上,利用∠B的正切值表示出PM、QN,然后根据梯形的面积公式列式整理即可得到S与t的函数关系式.
| 1 |
| 2 |
解答: 解:如图,过点C作CD⊥AB于D,
解:如图,过点C作CD⊥AB于D,
∵等边△ABC的边长为4厘米,
∴AD=BD=
AB=
×4=2,
①点N在AD上时,0≤t≤1,P、Q都在AC上,
∵MN=1,
∴AM=t,AN=t+1,
∴PM=AM•tan60°=
t,QN=AN•tan60°=
(t+1)=
t+
,
S=
(
t+
t+
)=
t+
;
②点N在BD上,点M在AD上时,1<t<2,点P在在AC上,点Q在BC上,
AM=t,BN=4-t-1=3-t,
PM=AM•tan60°=
t,QN=BN•tan60°=
(3-t)=3
-
t,
S=
(
t+3
-
t)=
;
③点M在BD上时,2≤t≤3,点P、Q都在BC上,
BM=4-t,BN=4-t-1=3-t,
PM=BM•tan60°=
(4-t)=4
-
t,QN=BN•tan60°=
(3-t)=3
-
t,
S=
(4
-
t+3
-
t)=-
t+
;
综上所述,四边形MNQP的面积为S=
,
函数图象为三段线段.
纵观各选项,只有A选项图形符合.
故选A.
 解:如图,过点C作CD⊥AB于D,
解:如图,过点C作CD⊥AB于D,∵等边△ABC的边长为4厘米,
∴AD=BD=
| 1 |
| 2 |
| 1 |
| 2 |
①点N在AD上时,0≤t≤1,P、Q都在AC上,
∵MN=1,
∴AM=t,AN=t+1,
∴PM=AM•tan60°=
| 3 |
| 3 |
| 3 |
| 3 |
S=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
②点N在BD上,点M在AD上时,1<t<2,点P在在AC上,点Q在BC上,
AM=t,BN=4-t-1=3-t,
PM=AM•tan60°=
| 3 |
| 3 |
| 3 |
| 3 |
S=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
3
| ||
| 2 |
③点M在BD上时,2≤t≤3,点P、Q都在BC上,
BM=4-t,BN=4-t-1=3-t,
PM=BM•tan60°=
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
S=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
7
| ||
| 2 |
综上所述,四边形MNQP的面积为S=
|
函数图象为三段线段.
纵观各选项,只有A选项图形符合.
故选A.
点评:本题考查了动点问题的函数图象,根据点P、Q所在的位置,确定出PM、QN的长度,然后利用梯形的面积公式列式得到S与t的函数关系式是解题的关键,也是本题的难点.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
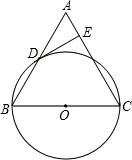 (2013•怀柔区二模)已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(2013•怀柔区二模)已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.