Question

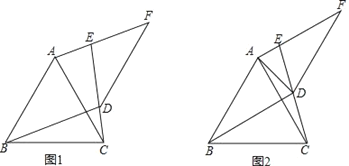
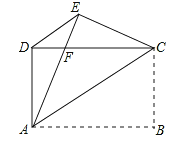
【题目】如图1，菱形中，，是对角线上的一点，点在的延长线上，且，交于，连接.

（1）证明：；

（2）判断的形状，并说明理由.

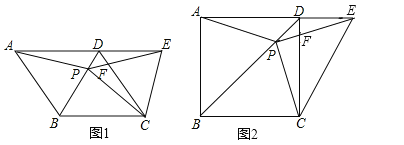
（3）如图2，把菱形改为正方形，其他条件不变，直接写出线段与线段的数量关系.

Answer 1

【答案】（1）证明见解析；（2）是等边三角形，理由见解析；（3）.

【解析】

（1）由菱形性质可知，，，即可证明；

（2）由△PDA≌△PDC，推出PA=PC，由PA=PE，推出，可知，由PA═PE=PC，即可证明△PEC是等边三角形；

（3）由△PDA≌△PDC，推出PA=PC，∠3=∠1，由PA=PE，推出∠2=∠3，推出∠1=∠2，由∠EDF=90°，∠DFE=∠PFC，推出∠FPC=EDF=90°，推出△PEC是等腰直角三角形即可解答；

（1）证明：在菱形中，，，

在和

，

∴.

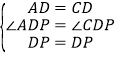（2）是等边三角形，

由（1）知，，∴，，

∵，∴，

∴，

∵（对顶角相等），

∴，

即，

又∵，；

∴，

∴是等边三角形.

（3）.

过程如下：证明：如图1中，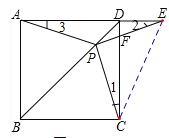

∵四边形ABCD是正方形，
∴AD=DC，∠ADB=∠CDB=45°，∠ADC=90°，
在△PDA和△PDC中，

，，
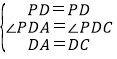∴△PDA≌△PDC，
∴PA=PC，∠3=∠1，
∵PA=PE，
∴∠2=∠3，
∴∠1=∠2，
∵∠EDF=90°，∠DFE=∠PFC，
∴∠FPC=EDF=90°，
∴△PEC是等腰直角三角形．

∴CE==.