Question

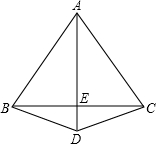如图，AB=AC=AD=4cm，DB=DC，若∠ABC为60度，则BE为________，∠ABD=________°．

Answer 1

2cm    75
分析：①由题意可得AE为中垂线，进而可得BE的长；②由等腰△ABD的两个底角相等、三角形内角和定理求得∠ABD=75°．
解答：①∵AB=AC，∠ABC为60度，
∴△ABC为等边三角形．
在△ABD和△ACD中，
∵，
∴△ABD≌△ACD，
∴∠BAD=∠CAD，
∴AE是BC边的中垂线，
∴BE=BC=2cm；
故答案是：2cm；
②∵AB=AD（已知），
∴∠ABD=∠ADB（等边对等角），
∴∠ABD=（180°-∠BAD）=（180°-30°）=75°．
故答案是：75．
点评：本题考查了等腰三角形的性质、等边三角形的判定与性质．等边三角形的三条边都相等，三个内角都是60°．