题目内容
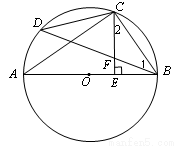
正六边形的边长为2,则它的边心距为_______.
【解析】
试题分析::连接OA、OB,根据正六边形的性质求出∠AOB,得出等边三角形OAB,求出OA、AM的长,根据勾股定理求出即可.连接OA、OB、OC、OD、OE、OF,

∵正六边形ABCDEF,
∴∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠AOF, ∴∠AOB=×360°=60°,OA=OB, ∴△AOB是等边三角形,
∴OA=OB=AB=2, ∵AB⊥CD, ∴AM=BM=1,
在△OAM中,由勾股定理得:OM=.
考点: 正多边形和圆;等边三角形的判定与性质;勾股定理.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目

 与y轴交于点C,与x轴交于点B,抛物线
与y轴交于点C,与x轴交于点B,抛物线 经过B、C两点,与x轴的正半轴交于另一点A,且OA :OC=2 :7.
经过B、C两点,与x轴的正半轴交于另一点A,且OA :OC=2 :7.

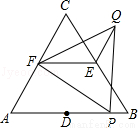
 的图象,下面四条信息:①a b c>0;②4a+c ?2b;③
的图象,下面四条信息:①a b c>0;②4a+c ?2b;③ ;④3b+2c <0,其中正确信息的个数是( )
;④3b+2c <0,其中正确信息的个数是( )
 B.
B.  C.
C.  D.
D. 




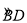 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.