Question

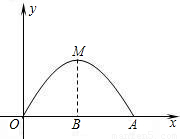
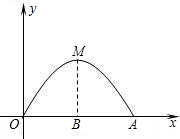有一个抛物线形的桥洞，桥洞离水面的最大高度BM为3米，跨度OA为6米，以OA所在直线为x轴，O为原点建立直角坐标系（如图所示）．
（1）请你直接写出O、A、M三点的坐标；
（2）一艘小船平放着一些长3米、宽2米且厚度均匀的矩形木板，要使该小船能通过此桥洞，问这些木板最高可堆放多少米（设船身底板与水面同一平面）？

Answer 1

分析：根据题意知M为抛物线的顶点，设抛物线顶点式，求解析式更方便；结合题意，就是已知自变量的值求函数值．

解答：解：（1）0（0，0），A（6，0），M（3，3）．
（2）设抛物线的关系式为y=a（x-3）²+3，
因为抛物线过点（0，0），
所以0=a（0-3）²+3，
解得a=-

1

3

，
所以y=-

1

3

（x-3）²+3=-

1

3

x²+2x，
要使木板堆放最高，依据题意，得B点应是木板宽CD的中点，
把x=2代入y=-

1

3

x²+2x，
得y=

8

3

，所以这些木板最高可堆放

8

3

米．

点评：本题考查点的坐标的求法及二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．