题目内容
在平面直角坐标系中,O是坐标原点,直角梯形AOCD的顶点A的坐标为
(0,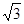 ),点D的坐标为(1,
),点D的坐标为(1,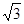 ),点C在
),点C在 轴的正半轴上,过点O且以点D为顶点的抛物线经过点C,点P为CD的中点.
轴的正半轴上,过点O且以点D为顶点的抛物线经过点C,点P为CD的中点.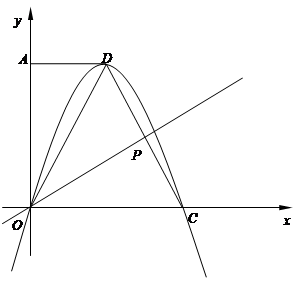
(1)求抛物线的解析式及点P的坐标;
(2) 在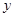 轴右侧的抛物线上是否存在点Q,使以Q为圆心的圆同时与
轴右侧的抛物线上是否存在点Q,使以Q为圆心的圆同时与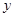 轴、直线OP相切.若存在,请求出满足条件的点Q的坐标;若不存在,请说明理由;
轴、直线OP相切.若存在,请求出满足条件的点Q的坐标;若不存在,请说明理由;
(3)点M为线段OP上一动点(不与O点重合),过点O、M、D的圆与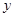 轴的正半轴交于点N.求证:OM+ON为定值.
轴的正半轴交于点N.求证:OM+ON为定值.
(4)在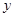 轴上找一点H,使∠PHD最大.试求出点H的坐标.
轴上找一点H,使∠PHD最大.试求出点H的坐标.
(1)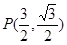 (2)
(2)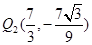 (3)H
(3)H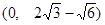
解析试题分析:解:(1) 设抛物线的解析式为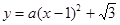 ,
,
将(0,0)代入,得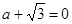 ,
,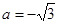
∴抛物线的解析式为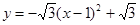 即
即 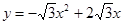 2分
2分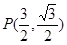 4分
4分
(2)若⊙Q在直线OP上方,则Q与D点重合,此时Q1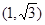 ;
;
若⊙Q在直线OP下方,与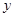 轴、直线OP切于E、F,
轴、直线OP切于E、F,
则QE=QF,QE⊥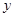 轴,QF⊥OP
轴,QF⊥OP
∴OQ平分∠EOF
∵∠EOF="120°" ∴∠FOQ=60°
∵∠POC=30°,则∠QOC=30°
设Q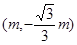 ,则
,则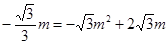
解得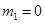 (舍去),
(舍去),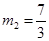 ∴
∴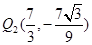 8分
8分
(3)∵在过点O、M、D的圆中,有∠MOD=∠NOD ∴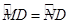 ∴MD= ND
∴MD= ND
易得OD平分∠AOP,DA⊥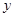 轴,DP⊥OP ∴DA= DP
轴,DP⊥OP ∴DA= DP
可证得△NAD≌△MPD(HL) ∴MP= AN
∴OM+ON= OP-MP+OA+AN=OP+OA=2OA=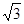 ,
,
则OM+ON=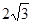 ,即OM+ON为定值. 11分
,即OM+ON为定值. 11分
(4)作过P、D两点且与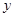 轴相切于点H的圆S,
轴相切于点H的圆S,
则由圆周角大于圆外角可知,∠PHD最大. 12分
设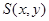 ,则由HS=SD=SP
,则由HS=SD=SP
可得,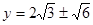
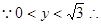 H
H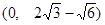 14分
14分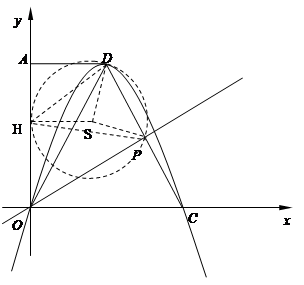
考点: 圆与二次函数
点评:此题比较综合,把几何图形和二次函数结合起来考察学生,要求学生都知识的掌握程度比较高,解答过程稍微比较复杂,是区分学生成绩的题目。

 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.