题目内容
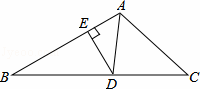
如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是 .
3
考点: 角平分线的性质.
分析: 过点D作DF⊥AC于F,根据角平分线上的点到角的两边距离相等可得DE=DF,再根据S△ABC=S△ABD+S△ACD列出方程求解即可.
解答: 解:如图,过点D作DF⊥AC于F,
∵AD是△ABC中∠BAC的角平分线,DE⊥AB,
∴DE=DF,
由图可知,S△ABC=S△ABD+S△ACD,
 ×4×2+
×4×2+ ×AC×2=7,
×AC×2=7,
解得AC=3.
故答案为3.

点评: 本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质是解题的关键.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 x+4的图象与x轴、y轴分别交于A,B两点,则线段AB的长为
x+4的图象与x轴、y轴分别交于A,B两点,则线段AB的长为  ,AC=8cm,AD=10cm,OD=OC=2cm,那么OB的长是( )
,AC=8cm,AD=10cm,OD=OC=2cm,那么OB的长是( )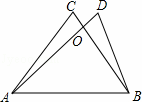
 .
.

 的系数是 ,次数是 次;多项式xy2﹣xy+24是 次 项式.
的系数是 ,次数是 次;多项式xy2﹣xy+24是 次 项式. ﹣1=
﹣1= .
.