题目内容
反比例函数y=
的图象是双曲线,在每一个象限内,y随x的增大而减小,若点A(-3,y1),B(-1,y2),C(2,y3)都在该双曲线上,则y1、y2、y3的大小关系为
| m | x |
y2<y1<y3
y2<y1<y3
.(用“<”号连接)分析:根据反比例函数的性质,图象在一、三象限,在双曲线的同一支上,y随x的增大而减小,则0>y1>y2,而y3>0,则可比较三者的大小.
解答:解:∵反比例函数y=
的图象是双曲线,在每一个象限内,y随x的增大而减小,
∴图象在一、三象限,
∵-3<-1,
∴0>y1>y2,
∵2>0,
∴y3>0,
∴y2<y1<y3,
故答案为:y2<y1<y3.
| m |
| x |
∴图象在一、三象限,
∵-3<-1,
∴0>y1>y2,
∵2>0,
∴y3>0,
∴y2<y1<y3,
故答案为:y2<y1<y3.
点评:本题考查了反比例函数图象上点的坐标特征,在反比函数中,已知各点的横坐标,比较纵坐标的大小,首先应区分各点是否在同一象限内.在同一象限内,按同一象限内点的特点来比较,不在同一象限内,按坐标系内点的特点来比较..

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
已知反比例函数y=
的图象经过点(-3a,-a),其中a≠0,则此反比例函数图象在( )
| m |
| x |
| A、第一,二象限 |
| B、第一,三象限 |
| C、第二,四象限 |
| D、第三,四象限 |
 如图,一次函数y=kx+b的图象与反比例函数
如图,一次函数y=kx+b的图象与反比例函数 两点.
两点.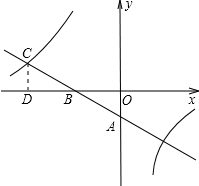 (2012•泰安)如图,一次函数y=kx+b的图象与坐标轴分别交于A,B两点,与反比例函数y=
(2012•泰安)如图,一次函数y=kx+b的图象与坐标轴分别交于A,B两点,与反比例函数y= 如图,一次函数y=kx+b的图象与反比例函数
如图,一次函数y=kx+b的图象与反比例函数