题目内容
下列四个解中是方程组
的解是( )
|
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
分析:把四个选项分别代入方程组,能使方程组中两个方程都成立的值,即是方程组的解.
解答:解:A、把
代入2x+31y=-11不成立,故不是方程组的解;
B、把
代入
x-y=6不成立,故不是方程组的解;
C、把
分别代入方程组的两个方程都成立,所以是方程组的解;
D、把
代入2x+31y=-11不成立,故不是方程组的解.
故选C.
|
B、把
|
| 1 |
| 2 |
C、把
|
D、把
|
故选C.
点评:此题主要考查了二元一次方程组解的定义.所谓“方程组”的解,指的是该数值满足方程组中的每一方程的值.

练习册系列答案
相关题目
 的解是
的解是


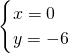
 的解是( )
的解是( )