��Ŀ����
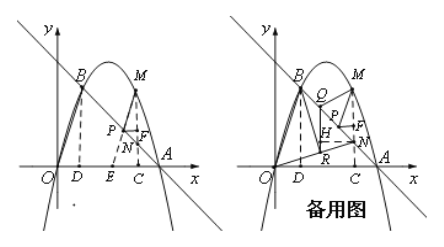
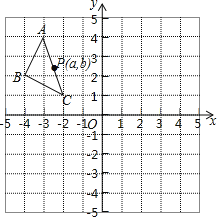
����Ŀ����ͼ����ƽ��ֱ�������У���OΪ����ԭ�㣬ֱ��y=��x+4��x�ύ�ڵ�A������A��������y=ax2+bx��ֱ��y=��x+4������һ��B���ҵ�B�ĺ�����Ϊ1��
��1����a��b��ֵ��
��2����P���߶�AB��һ���㣨��P�����A��B�غϣ�������P��PM��OB����һ�����ڵ��������ڵ�M������M��MC��x���ڵ�C����AB�ڵ�N������P��PF��MC�ڵ�F����PF�ij�Ϊt��MN�ij�Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£���S��ACN=S��PMNʱ������ON����Q���߶�BP�ϣ�����Q��QR��MN��ON�ڵ�R������MQ��BR������MQR����BRN=45��ʱ�����R�����꣮
���𰸡���1��a=��1��b=4��
��2��d=3t+t=4t��
��3��R��![]() ��
��![]() ����
����
��������
�����������1������֪�ɵó�A��B�����꣬�Ӷ����ݴ���ϵ�����ó�a��b��ֵ��
��2������֪�ɵó�AD=BD���Ӷ���BAD=��ABD=45���������ɵó�tan��BOD=tan��MPF����![]() =3��MF=3PF=3t�����ɵó�d��t�ĺ�����ϵ��
=3��MF=3PF=3t�����ɵó�d��t�ĺ�����ϵ��
��3����S��ACN=S��PMN����ɵ�![]() AC2=2t2���Ӷ��ó�AC=2t��CN=2t����M��4��2t��6t�������t��ֵ�������ó���PMQ�ס�NBR�����R�����꣮
AC2=2t2���Ӷ��ó�AC=2t��CN=2t����M��4��2t��6t�������t��ֵ�������ó���PMQ�ס�NBR�����R�����꣮
�����������1����y=��x+4��x�ύ�ڵ�A��
��A��4��0����
����B�ĺ�����Ϊ1����ֱ��y=��x+4������B��
��B��1��3����
��������y=ax2+bx����A��4��0����B��1��3����
��![]() ��
��
��ã�![]() ��
��
��a=��1��b=4��
��2����ͼ����BD��x���ڵ�D���ӳ�MP��x���ڵ�E��
��B��1��3����A��4��0����
��OD=1��BD=3��OA=4��
��AD=3��
��AD=BD��
�ߡ�BDA=90������BAD=��ABD=45����
��MC��x�ᣬ���ANC=��BAD=45����
���PNF=��ANC=45����
��PF��MC�����FPN=��PNF=45����
��NF=PF=t��
�ߡ�DFM=��ECM=90������PF��EC��
���MPF=��MEC��
��ME��OB�����MEC=��BOD��
���MPF=��BOD��
��tan��BOD=tan��MPF��
��![]() =3��
=3��
��MF=3PF=3t��
��MN=MF+FN��
��d=3t+t=4t��
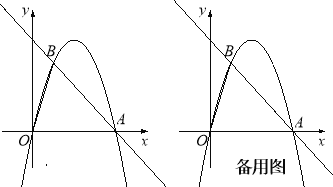
��3���籸��ͼ���ɣ�2��֪��PF=t��MN=4t��
��S��PMN=![]() MN��PF=
MN��PF=![]() ��4t��t=2t2��
��4t��t=2t2��
�ߡ�CAN=��ANC��
��CN=AC��
��S��ACN=![]() AC2��
AC2��
��S��ACN=S��PMN��
��![]() AC2=2t2��
AC2=2t2��
��AC=2t����CN=2t��
��MC=MN+CN=6t��
��OC=OA��AC=4��2t��
��M��4��2t��6t����
�ɣ�1��֪�����ߵĽ���ʽΪ��y=��x2+4x��
��M��4��2t��6t������y=��x2+4x�ã�
����4��2t��2+4��4��2t��=6t��
��ã�t1=0���ᣩ��t2=![]() ��
��
��PF=NF=![]() ��AC=CN=1��OC=3��MF=
��AC=CN=1��OC=3��MF=![]() ��PN=
��PN=![]() ��PM=
��PM=![]() ��AN=
��AN=![]() ��
��
��AB=3![]() ��
��
��BN=2![]() ��
��
��NH��RQ�ڵ�H��
��QR��MN��
���MNH=��RHN=90����
��RQN=��QNM=45�������MNH=��NCO��
��NH��OC��
���HNR=��NOC��
��tan��HNR=tan��NOC��
��![]() ��
��
��RH=n����HN=3n��
��RN=![]() n��QN=3
n��QN=3![]() n��
n��
��PQ=QN��PN=3![]() n��
n��![]() ��
��
��ON=![]() ��
��
OB=![]() ��
��
��OB=ON�����OBN=��BNO��
��PM��OB��
���OBN=��MPB��
���MPB=��BNO��
�ߡ�MQR����BRN=45������MQR=��MQP+��RQN=��MQP+45����
���BRN=��MQP��
���PMQ�ס�NBR��
��![]() ��
��
��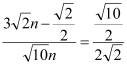 ��
��
��ã�n=![]() ��
��
��R�ĺ�����Ϊ��3��![]() ��R��������Ϊ��1��
��R����������1��![]() =
=![]() ��
��
��R��![]() ��
��![]() ����
����