Question

数学课上，张老师给出了问题：如图（1），四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角∠DCG的平分线CF 于点F，求证：AE=EF。
经过思考，小明展示了一种正确的解题思路：取AB 的中点M，连接ME，则AM=EC，易证△AME≌△ECF，所以AE=EF，在此基础上，同学们作了进一步探究：
（1）小颖提出：如图（2），如果把“点E是边BC的中点” 改为“点E是边BC上（除B、C外）的任意一点”，其他条件不变，那么结论“AE= EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；
（2）小华提出：如图（3），点E是BC的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE=EF” 仍然成立，你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由。

Answer 1

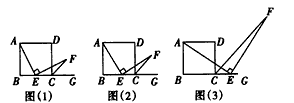
解：（1）正确， 证明：如图（1），在AB上取一点M，使AM=EC，连接ME， ∴BM=BE， ∴∠BME=45°， ∴∠AME=135°， ∵CF是正方形外角∠DCG的平分线，　 ∴∠DCF=45°，　 ∴∠BCF=135°，　 ∴∠AME=∠ECF， ∵∠AEB+∠BAE=90°，∠AEB+∠CEF=90°， ∴∠BAE=∠CEF， ∴△AME≌△ECF（ASA）， ∴AE=EF；
（2）正确， 证明：如图（2）， 在BA的延长线上取一点N，使AN=CE，连接NE， ∴BN=BE， ∴∠N=∠FCE=45°， ∵四边形ABCD是正方形， ∴AD∥BE， ∴∠DAE=∠BEA， ∴∠NAE=∠CEF， ∴△ANE≌△ECF（ASA）， ∴AE=EF。