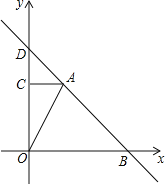题目内容
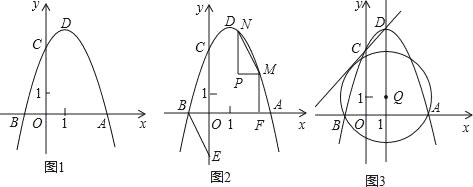
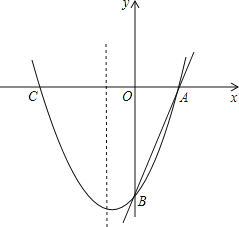
【题目】反比例函数![]() 的图象经过点
的图象经过点![]() 点是直线
点是直线![]() 上一个动点,如图所示,设
上一个动点,如图所示,设![]() 点的横坐标为
点的横坐标为![]() 且满足
且满足![]() 过
过![]() 点分别作
点分别作![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 与双曲线分别交于
与双曲线分别交于![]() 两点,连结
两点,连结![]() .
.
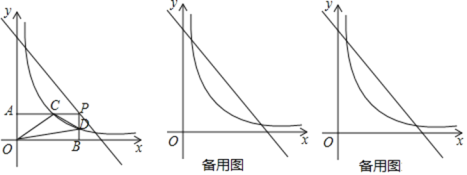
(1)求![]() 的值并结合图像求出
的值并结合图像求出![]() 的取值范围;
的取值范围;
(2)在![]() 点运动过程中,求线段
点运动过程中,求线段![]() 最短时点
最短时点![]() 的坐标;
的坐标;
(3)将三角形![]() 沿着
沿着![]() 翻折,点
翻折,点![]() 的对应点
的对应点![]() 得到四边形
得到四边形![]() 能否为菱形?若能,求出
能否为菱形?若能,求出![]() 点坐标;若不能,说明理由;
点坐标;若不能,说明理由;
(4)在![]() 点运动过程中使得
点运动过程中使得![]() 求出此时
求出此时![]() 的面积.
的面积.
【答案】(1)![]() ,
,![]() ,(2)
,(2)![]() ,(3)能,
,(3)能,![]() ,
,
(4)![]()
【解析】
(1)先把(1,3)代入![]() 求出k的值,再由两函数有交点求出m的值,根据函数图象即可得出结论;
求出k的值,再由两函数有交点求出m的值,根据函数图象即可得出结论;
(2)根据线段OC最短可知OC为∠AOB的平分线,对于![]() ,令
,令![]() ,即可得出C点坐标,把
,即可得出C点坐标,把![]() 代入
代入![]() 中求出
中求出![]() 的值即可得出P点坐标;
的值即可得出P点坐标;
(3)当OC=OD时,四边形O′COD为菱形,由对称性得到△AOC≌△BOD,即OA=OB,由此时P横纵坐标相等且在直线![]() 上即可得出结论.
上即可得出结论.
(4)设![]() ,则
,则![]() ,
,![]() ,根据PD=DB,构建方程求出
,根据PD=DB,构建方程求出![]() ,即可解决问题.
,即可解决问题.
解:(1)∴反比例函数![]() (x>0,k≠0)的图象进过点(1,3),
(x>0,k≠0)的图象进过点(1,3),
∴把(1,3)代入![]() ,解得
,解得![]() ,
,
![]() .
.
∵ ![]() ,
,
∴![]() ,
,
![]() ,
,
∴由图象得:![]() ;
;
(2)∵线段OC最短时,
∴OC为∠AOB的平分线,
∵对于![]() ,令
,令![]() ,
,
∴![]() ,即C
,即C![]() ,
,
∴把![]() 代入
代入![]() 中,得:
中,得:![]() ,即P
,即P![]() ;
;
(3)四边形O′COD能为菱形,
∵当OC=OD时,四边形O′COD为菱形,
∴由对称性得到△AOC≌△BOD,即OA=OB,
∴此时P横纵坐标相等且在直线![]() 上,
上,
即![]() ,解得:
,解得:![]() ,即P
,即P![]() .
.
(4)设B![]() ,则
,则![]() ,
,
∵PD=DB,
∴![]() ,
,
解得:![]() (舍弃),
(舍弃),
∴![]() ,D
,D![]() ,
,![]() ,
,![]() ,
,
![]()

 名校课堂系列答案
名校课堂系列答案【题目】大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
x(天) | 1 | 2 | 3 | … | 50 |
p(件) | 118 | 116 | 114 | … | 20 |
销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时q=40+![]() .
.
(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
(3)这50天中,该超市第几天获得利润最大?最大利润为多少?