题目内容

甲、乙、丙、丁四名射击运动员参加了预选赛，他们射击成绩的平均环数 $数学公式$ 及方差s²如表所示．
甲乙丙丁
$数学公式$ 8 9 9 8
s² 1 1 1.2 1.3
如果选出一个成绩较好且状态稳定的运动员去参赛，那么应选

A.
甲
B.
乙
C.
丙
D.
丁

B
分析：先比较平均数，乙丙的平均成绩好且相等，再比较方差即可解答．
解答：由图可知，乙、丙的平均成绩好，
由于S²_乙＜S²_丙，故丙的方差大，波动大．
故选B．
点评：本题考查方差的定义与意义：一般地设n个数据，x₁，x₂，…x_n的平均数为 $\text{[math]}$ ，则方差S²= $\text{[math]}$ [（x₁- $\text{[math]}$ ）²+（x₂- $\text{[math]}$ ）²+…+（x_n- $\text{[math]}$ ）²]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．

练习册系列答案

口算题卡河北少年儿童出版社系列答案

黄冈状元成才路口算题卡系列答案

趣味数学口算题卡系列答案

同步口算题卡系列答案

天天练口算题卡系列答案

口算题卡延边大学出版社系列答案

英才教程奇迹课堂口算题卡系列答案

A加金题系列答案

学习方案系列答案

全优测试卷系列答案

相关题目

已知：在Rt△ABC中∠C=90°，CD为AB边上的高．
求证：Rt△ADC∽Rt△CDB．

如图，MN是梯形ABCD的中位线，若CD=2，AB=6，则MN的长是

A.
2
B.
3
C.
4
D.
5

如图，以Rt△ABC的直角边AC所在的直线为轴，将△ABC旋转一周，所形成的几何体的俯视图是

A.
B.
C.
D.

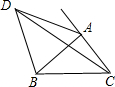如图，在△ABC中，∠A=60°，∠C=80°，∠C的平分线与∠A的外角平分线交于D，连接BD，则tan∠BDC的值是

A.
1
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

与-8的积为1的数是

A.
-8
B.
8
C.
$数学公式$
D.
- $数学公式$

一组数据：0，1，2，3，3，5，5，10的中位数是

A.
2.5
B.
3
C.
3.5
D.
5

如果 $数学公式$ 是数a的立方根，- $数学公式$ 是b的一个平方根，则a¹⁰×（-b）⁹等于

A.
2
B.
-2
C.
1
D.
1

如图圆O直径AB上一点P，AB=2，∠BAC=20°，D是弧BC中点，则PD+PC的最小值为

A.
$数学公式$
B.
1
C.
$数学公式$
D.
$数学公式$