题目内容
如图所示,在△ABC 中,BA=BC=20cm ,AC=30cm ,点P 从点A 出发,沿AB 以每秒4cm ,的速度向点B 运动,同时点Q 从C 点出发,沿CA 以3cm/s 的速度向点A 运动,设运动时间为x 秒。

(1 )当x 为何值时,BP=BQ ;
(2 )当x 为何值时,PQ ∥BC ;
(3 )△APQ 能否与△CQB 相似,若能,求出x 的值,若不能,请说明理由。
(2 )当x 为何值时,PQ ∥BC ;
(3 )△APQ 能否与△CQB 相似,若能,求出x 的值,若不能,请说明理由。
解: (1 )依题意可得:BP=20 -4x,CQ=3x
当BP=CQ时,20-4x =3x
∴x= (秒)
(秒)
答:当x= 秒时,BP=CQ;
秒时,BP=CQ;

(2 )AP=4x,AB=20,AQ=30-3x,AC=30
所以当PQ‖BC 时,有
即:
解得:x= (秒)
(秒)
答:当x= 秒时,PQ‖BC ;
秒时,PQ‖BC ;
(3 )能。
①当△APQ ∽△CQB 时,有
即:
解得:x= (秒)
(秒)
②当△APQ∽△CBQ时,有
即:
解得:x=5(秒)或x=-10(秒)(舍去)
答:当x= 秒或x=5秒时,△APQ与△CQB相似。
秒或x=5秒时,△APQ与△CQB相似。
当BP=CQ时,20-4x =3x
∴x=
 (秒)
(秒)答:当x=
 秒时,BP=CQ;
秒时,BP=CQ;
(2 )AP=4x,AB=20,AQ=30-3x,AC=30
所以当PQ‖BC 时,有

即:

解得:x=
 (秒)
(秒)答:当x=
 秒时,PQ‖BC ;
秒时,PQ‖BC ;(3 )能。
①当△APQ ∽△CQB 时,有

即:

解得:x=
 (秒)
(秒) ②当△APQ∽△CBQ时,有

即:

解得:x=5(秒)或x=-10(秒)(舍去)
答:当x=
 秒或x=5秒时,△APQ与△CQB相似。
秒或x=5秒时,△APQ与△CQB相似。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 如图所示,在△ABC中,∠A=47°,∠C=77°,DE∥BC,BF平分∠ABC,BF交DE于点F,求∠BFE的度数.
如图所示,在△ABC中,∠A=47°,∠C=77°,DE∥BC,BF平分∠ABC,BF交DE于点F,求∠BFE的度数.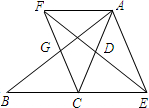 如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.
如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF. 15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=
15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=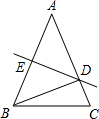 如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为
如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为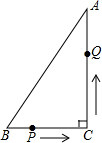 如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.
如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.