Question

【题目】如图，直线AB的函数解析式为y=-2x+8，与x轴交于点A，与y轴交于点B。

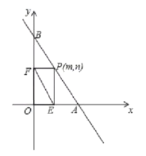
（1）求A、B两点的坐标；

（2）若点P（m,n）为线段AB上的一个动点（与A、B不重合），作PE⊥x轴于点E，PF⊥y轴于点F，连接E，若△PAO的面积为S，求S关于m的函数关系式，并写出m的取值范围。

Answer 1

【答案】（1）A(4,0)，B(0,8)；（2）S△PAO=4m+16(0<m<4)；

【解析】

（1）利用待定系数法即可解决问题；

（2）连接OP，根据三角形的面积公式S△PAO=×OA×PE计算即可；

(1)令x=0，则y=8，

∴B(0,8)，

令y=0,则2x+8=0,

∴x=4，

∴A(4,0)，

(2)连接OP.

∵点P(m,n)为线段AB上的一个动点，

∴2m+8=n,∵A(4,0)，

∴OA=4，

∴0<m<4

∴S△PAO=×OA×PE=×4×n=2(2m+8)=4m+16(0<m<4)；