题目内容
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.例如:由图1可得到![]() .
.

(1)写出由图2所表示的数学等式:________.

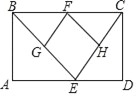
(2)写出由图3所表示的数学等式:________.

(3)已知实数![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() .
.
①求![]() 的值.
的值.
②求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①0 ;②1.
;(3)①0 ;②1.
【解析】
(1)根据数据表示出正方形的边长,再根据正方形的面积公式写出等式的左边,再表示出每一小部分的面积,然后根据面积相等即可写出等式;
(2)根据数据表示出阴影正方形的边长,再根据正方形的面积公式写出等式的左边,再用大正方形的面积减去其他八小部分的面积,然后根据面积相等即可写出等式;
(3)①根据(1)的结论变形为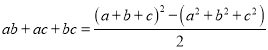 ,代数求值即可得解;
,代数求值即可得解;
②在①的基础上即可求得![]() 的值.
的值.
解:(1)∵大正方形的边长为![]()
∴大正方形的面积可表示为![]()
∵观察图形可知九小部分的面积和为![]()
![]()
∴由图2所表示的数学等式:![]() ;
;
(2)∵阴影正方形的边长为![]()
∴阴影正方形的面积为![]()
∵阴影正方形的面积还以表示为大正方形的面积减去其他八小部分的面积:
![]()
∴由图3所表示的数学等式:![]() ;
;
(3)①∵由图2所表示的数学等式:![]()
∴![]()
∴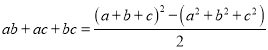
∵![]() ,
,![]()
∴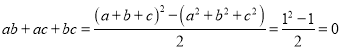 ,即
,即![]() ;
;
②∵![]() ,
,![]()
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目