题目内容
【题目】如图，已知在梯形ABCD中，AD∥BC，AB=AD=5，tan∠DBC=
．点E为线段BD上任意一点（点E与点B，D不重合），过点E作EF∥CD，与BC相交于点F，连接CE．设BE=x，y=
．
（1）求BD的长；
（2）如果BC=BD，当△DCE是等腰三角形时，求x的值；
（3）如果BC=10，求y关于x的函数解析式，并写出自变量x的取值范围．
【答案】（1）8；（2）
；（3）
（0＜x＜8）．
【解析】
试题分析：（1）过A作AH⊥BD于H，再根据AD∥BC，AB=AD=5，可得∠ABD=∠ADB=∠DBC，BH=HD，再根据tan∠ABD= tan∠DBC=
，计算出BH=DH=4，进而得到BD=8；
（2）分两种情况用锐角三角函数计算即可得出结论．
（3）首先利用平行线的性质得出△FEB∽△CDB，即可得出y与x的函数关系式；
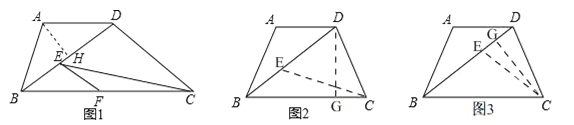
试题解析：（1）如图1，过A作AH⊥BD于H，∵AD∥BC，AB=AD=5，∴∠ABD=∠ADB=∠DBC，BH=HD，在Rt△ABH中，∵tan∠ABD=tan∠DBC=，∴cos∠ABD=
，∴BH=DH=4，∴BD=8；
（2）∵△DCE是等腰三角形，且BC=BD=8，∴①如图2，当CD=DE时，即：CD=DE=BD﹣BE=8﹣x，过点D作DG⊥BC于G，在Rt△BDG中，tan∠DBC=，BD=8，∴DG=
BD=
，BG=
BD=
，∴CG=8﹣BG=
，在Rt△CDG中，根据勾股定理得，DG2+CG2=CD2，∴
，∴x=
（舍）或x=
；
②如图3，当CE=CD时，过点C作CG⊥BD，∴DG=EG=
DE，在Rt△BCG中，BC=8，tan∠DBC=，∴BG=，∴DG=BD﹣BG=
，∴x=BE=BD﹣DE=BD﹣2DG=．
（3）∵BF=x，BC=10，∴FC=10﹣x，∴
=
=
，∵EF∥DC，∴△FEB∽△CDB，∴
=
，∴
=
=
（0＜x＜8），∴（0＜x＜8）．
