题目内容
 如图,抛物线y=ax2+bx+c与x轴有两个不同的交点A(x1,0)、B(x2,0)(x1<x2),与y轴的正半轴交于点C(0,3).已知该抛物线的顶点横坐标为1,A、B两点间的距离为4.
如图,抛物线y=ax2+bx+c与x轴有两个不同的交点A(x1,0)、B(x2,0)(x1<x2),与y轴的正半轴交于点C(0,3).已知该抛物线的顶点横坐标为1,A、B两点间的距离为4.
(1)求这条抛物线的解析式;
(2)求△ABC外接圆的圆心M的纵坐标;
(3)在抛物线上是否存在一点P,使△PBD(PD垂直于x轴,垂足为D)被直线BM分成面积比为1:2两部分?若存在,请求出点P的坐标;若不存在,请说明理由.
解:(1)∵抛物线y=ax2+bx+c与x轴有两个不同的交点A(x1,0)、B(x2,0)(x1<x2),且抛物线顶点的横坐标为1,
∴ =1,即x1+x2=2①;
=1,即x1+x2=2①;
又∵A、B两点间的距离为4,且x1<x2,
∴x2-x1=4②,
①与②组成方程组 ,
,
解得 ,
,
∴A(-1,0),B(3,0).
把A(-1,0),B(3,0),C(0,3)代入y=ax2+bx+c,
得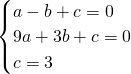 ,
,
解得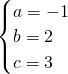 ,
,
∴函数解析式为y=-x2+2x+3;
(2)∵△ABC外接圆的圆心是M,
∴MA=MB=MC,M点在线段AB的垂直平分线上,
∵A(-1,0),B(3,0),
∴M的横坐标为: =1.
=1.
设M(1,y),由MA=MC,
得(1+1)2+y2=12+(y-3)2,
解得y=1.
故△ABC外接圆的圆心M的纵坐标为1;
 (3)在抛物线上存在一点P,能够使△PBD(PD垂直于x轴,垂足为D)被直线BM分成面积比为1:2的两部分.理由如下:
(3)在抛物线上存在一点P,能够使△PBD(PD垂直于x轴,垂足为D)被直线BM分成面积比为1:2的两部分.理由如下:
设PD与BM的交点为E,可求直线BM解析式为y=- x+
x+ ,
,
设P(x,-x2+2x+3),分两种情况:
①当S△BED:S△BEP=1:2时,PD=3DE,如图.
则-x2+2x+3=3(- x+
x+ ),
),
整理,得2x2-7x+3=0,
解得x= 或3,
或3,
∴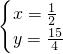 或
或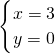 (舍去),
(舍去),
∴P( ,
, );
);
 ②当S△PBE:S△BED=1:2时,2PD=3DE,如图.
②当S△PBE:S△BED=1:2时,2PD=3DE,如图.
则2(-x2+2x+3)=3(- x+
x+ ),
),
整理,得4x2-11x-3=0,
解得x=- 或3,
或3,
∴ 或
或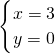 (舍去),
(舍去),
∴P(- ,
,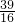 ).
).
故在抛物线上存在点P( ,
, )或P(-
)或P(- ,
,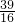 ),使△PBD(PD垂直于x轴,垂足为D)被直线BM分成面积比为1:2的两部分.
),使△PBD(PD垂直于x轴,垂足为D)被直线BM分成面积比为1:2的两部分.
分析:(1)因为抛物线y=ax2+bx+c与x轴有两个不同的交点A(x1,0),B(x2,0)(x1<x2),所以A和B关于抛物线的对称轴对称,于是 =1①;又因为A、B两点间的距离为4,且x1<x2,所以x2-x1=4②,将①②组成方程组,解出x1,x2的值,再将点A、B、C的坐标代入y=ax2+bx+c,运用待定系数法即可求出抛物线的解析式;
=1①;又因为A、B两点间的距离为4,且x1<x2,所以x2-x1=4②,将①②组成方程组,解出x1,x2的值,再将点A、B、C的坐标代入y=ax2+bx+c,运用待定系数法即可求出抛物线的解析式;
(2)根据三角形外心的定义可知MA=MB=MC,由MA=MB及A、B两点的坐标,得出圆心M的横坐标为1,设M(1,y),根据MA=MC列出方程,即可求出M的纵坐标;
(3)设PD与BM的交点为E,分成两种情况考虑:①当△BPE的面积是△BDE的2倍时,由于△BDE和△BPD同高不等底,那么它们的面积比等于底边的比,即DE= PD,可设出P点的坐标,那么E点的纵坐标是P点纵坐标的
PD,可设出P点的坐标,那么E点的纵坐标是P点纵坐标的 ,BD的长为B、P横坐标差的绝对值,由于∠OBC=45°,那么BD=DE,可以此作为等量关系求出P点的坐标;②当△BDE的面积是△BPE的2倍时,方法同①.
,BD的长为B、P横坐标差的绝对值,由于∠OBC=45°,那么BD=DE,可以此作为等量关系求出P点的坐标;②当△BDE的面积是△BPE的2倍时,方法同①.
点评:此题是二次函数的综合类题目,其中涉及到运用待定系数法求函数的解析式,二次函数的性质,三角形的外心,两点间的距离公式以及图形面积的求法等知识,综合性强,难度稍大,(3)中进行分类讨论是解题的关键.
∴
 =1,即x1+x2=2①;
=1,即x1+x2=2①;又∵A、B两点间的距离为4,且x1<x2,
∴x2-x1=4②,
①与②组成方程组
 ,
,解得
 ,
,∴A(-1,0),B(3,0).
把A(-1,0),B(3,0),C(0,3)代入y=ax2+bx+c,
得
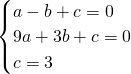 ,
,解得
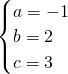 ,
,∴函数解析式为y=-x2+2x+3;
(2)∵△ABC外接圆的圆心是M,
∴MA=MB=MC,M点在线段AB的垂直平分线上,
∵A(-1,0),B(3,0),
∴M的横坐标为:
 =1.
=1.设M(1,y),由MA=MC,
得(1+1)2+y2=12+(y-3)2,
解得y=1.
故△ABC外接圆的圆心M的纵坐标为1;
 (3)在抛物线上存在一点P,能够使△PBD(PD垂直于x轴,垂足为D)被直线BM分成面积比为1:2的两部分.理由如下:
(3)在抛物线上存在一点P,能够使△PBD(PD垂直于x轴,垂足为D)被直线BM分成面积比为1:2的两部分.理由如下:设PD与BM的交点为E,可求直线BM解析式为y=-
 x+
x+ ,
,设P(x,-x2+2x+3),分两种情况:
①当S△BED:S△BEP=1:2时,PD=3DE,如图.
则-x2+2x+3=3(-
 x+
x+ ),
),整理,得2x2-7x+3=0,
解得x=
 或3,
或3,∴
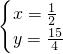 或
或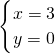 (舍去),
(舍去),∴P(
 ,
, );
); ②当S△PBE:S△BED=1:2时,2PD=3DE,如图.
②当S△PBE:S△BED=1:2时,2PD=3DE,如图.则2(-x2+2x+3)=3(-
 x+
x+ ),
),整理,得4x2-11x-3=0,
解得x=-
 或3,
或3,∴
 或
或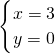 (舍去),
(舍去),∴P(-
 ,
,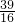 ).
).故在抛物线上存在点P(
 ,
, )或P(-
)或P(- ,
,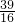 ),使△PBD(PD垂直于x轴,垂足为D)被直线BM分成面积比为1:2的两部分.
),使△PBD(PD垂直于x轴,垂足为D)被直线BM分成面积比为1:2的两部分.分析:(1)因为抛物线y=ax2+bx+c与x轴有两个不同的交点A(x1,0),B(x2,0)(x1<x2),所以A和B关于抛物线的对称轴对称,于是
 =1①;又因为A、B两点间的距离为4,且x1<x2,所以x2-x1=4②,将①②组成方程组,解出x1,x2的值,再将点A、B、C的坐标代入y=ax2+bx+c,运用待定系数法即可求出抛物线的解析式;
=1①;又因为A、B两点间的距离为4,且x1<x2,所以x2-x1=4②,将①②组成方程组,解出x1,x2的值,再将点A、B、C的坐标代入y=ax2+bx+c,运用待定系数法即可求出抛物线的解析式;(2)根据三角形外心的定义可知MA=MB=MC,由MA=MB及A、B两点的坐标,得出圆心M的横坐标为1,设M(1,y),根据MA=MC列出方程,即可求出M的纵坐标;
(3)设PD与BM的交点为E,分成两种情况考虑:①当△BPE的面积是△BDE的2倍时,由于△BDE和△BPD同高不等底,那么它们的面积比等于底边的比,即DE=
 PD,可设出P点的坐标,那么E点的纵坐标是P点纵坐标的
PD,可设出P点的坐标,那么E点的纵坐标是P点纵坐标的 ,BD的长为B、P横坐标差的绝对值,由于∠OBC=45°,那么BD=DE,可以此作为等量关系求出P点的坐标;②当△BDE的面积是△BPE的2倍时,方法同①.
,BD的长为B、P横坐标差的绝对值,由于∠OBC=45°,那么BD=DE,可以此作为等量关系求出P点的坐标;②当△BDE的面积是△BPE的2倍时,方法同①.点评:此题是二次函数的综合类题目,其中涉及到运用待定系数法求函数的解析式,二次函数的性质,三角形的外心,两点间的距离公式以及图形面积的求法等知识,综合性强,难度稍大,(3)中进行分类讨论是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).