题目内容
如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.

(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
(1)AE=CF (2)∠EGC=80°
【解析】
试题分析:(1)要证AE=CF,若我们能够证明其所在的三角形全等即可。AE位于
△AEB中,CF位于△CFB中,因为四边形ABCD是正方形,则AB=BC,因为
BE⊥BF,则∠ABC=∠EBF=90°,都减去∠EBC,故∠ABE=∠CBF,又因为BE=BF,故可以
由SAS定理得到两个三角形全等。故AE=CF。
(2)由三角形的外角等于和他不相邻的两个内角之和,则∠EGC=∠EBG+∠BEF,由BE⊥BF,
∠FBE=90°,BE=BF,则∠BEF=∠EFB=45°,而∠EBG=90°-∠ABE=90°-55°=35°,故可求出∠EGC=80°。
试题解析:
(1)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC, 1分
∵BE⊥BF,
∴∠FBE=90°,
∵∠ABE+∠EBC=90°,∠CBF+∠EBC=90°,
∴∠ABE=∠CBF, 2分
在△AEB和△CFB中,

∴△AEB≌△CFB(SAS), 4分
∴AE=CF. .5分
(2)【解析】
∵BE⊥BF,
∴∠FBE=90°,
又∵BE=BF,
∴∠BEF=∠EFB=45°,
∵四边形ABCD是正方形,
∴∠ABC=90°,
又∵∠ABE=55°,
∴∠EBG=90°-55°=35°, 7分
∴∠EGC=∠EBG+∠BEF=45°+35°=80° 9分
考点:1.三角形全等的判定定理 2.正方形的性质 3.角形的外角等于和他不相邻的两个内角之和

练习册系列答案
相关题目
 (元/台)与采购数量
(元/台)与采购数量 (台)满足
(台)满足 (
( ,
, (元/台)与采购数量
(元/台)与采购数量 (台)满足
(台)满足 (
( ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案?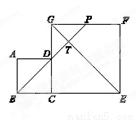
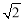 B.
B.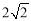 C.2 D.1
C.2 D.1


