题目内容
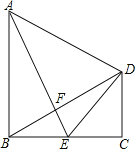
【题目】如图①,![]() 中,
中,![]() ,
,![]() 、∠C的平分线交于
、∠C的平分线交于![]() 点,过
点,过![]() 点作
点作![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() .试回答:
.试回答:
(1)图中等腰三角形有________个.猜想:![]() 与
与![]() 、
、![]() 之间的关系是________.说明理由;
之间的关系是________.说明理由;
(2)如图②,若![]() ,图中等腰三角形有________个,在第(1)问中
,图中等腰三角形有________个,在第(1)问中![]() 与
与![]() 、
、![]() 间的关系还存在吗?
间的关系还存在吗?
(3)如图③,若![]() 中
中![]() 的平分线
的平分线![]() 与三角形外角平分线
与三角形外角平分线![]() 交于
交于![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,这时图中还有等腰三角形吗?
,这时图中还有等腰三角形吗?![]() 与
与![]() 、
、![]() 关系又如何?说明你的理由.
关系又如何?说明你的理由.
【答案】(1) 5个,![]() ;(2)见解析;(3) 见解析.
;(2)见解析;(3) 见解析.
【解析】
(1)根据等腰三角形的判定、平分线的性质及角平分线可得有5个等腰三角形, 由△EOB和△FOC是等腰三角形,则EO=BE,OF=FC,则EF=BE+FC;
(2)由(1)的证明过程可知:在证△OEB、△OFC是等腰三角形的过程中,与AB=AC的条件没有关系,故这两个等腰三角形还成立.所以(1)中得出的EF=BE+FC的结论仍成立.
(3)思路与(2)相同,只不过结果变成了EF=BE-FC.
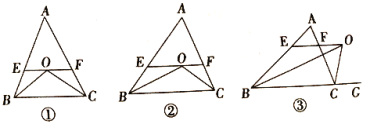
解:(1)如图1,图中共有5个等腰三角形,分别是△AEF、△OEB、△OFC、△OBC、△ABC;
理由是:∵AB=AC,
∴∠ACB=∠ABC,△ABC是等腰三角形;
∵BO、CO分别平分∠ABC和∠ACB,
∴∠ABO=∠OBC=![]() ∠ABC,∠OCB=∠ACO=
∠ABC,∠OCB=∠ACO=![]() ∠ACB,
∠ACB,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠ABO=∠OBC=∠EOB=∠OCB=∠FOC=∠FCO,
∴△EOB、△OBC、△FOC都是等腰三角形,
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠AEF=∠AFE,
∴△AEF是等腰三角形,
∴图中是等腰三角形的有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
![]() 、
、![]() 、
、![]() 的关系是
的关系是![]() .理由如下:
.理由如下:
∵![]() 、
、![]() 平分
平分![]() 、
、![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
∴![]() .
.
(2)2个
存在(1)的结论仍然成立.(证明过程同(1)).
(3)![]() 和
和![]() 仍是等腰三角形,
仍是等腰三角形,![]() .理由如下:
.理由如下:
同(1)可证得![]() 是等腰三角形.
是等腰三角形.
∵![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,故
,故![]() 是等腰三角形,
是等腰三角形,
∴![]() .
.

【题目】小颖和小红两位同学在学习“概率”时,做掷骰子(质地均匀的正方体)实验.
![]() 他们在一次实验中共掷骰子
他们在一次实验中共掷骰子![]() 次,试验的结果如下:
次,试验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
①填空:此次实验中“![]() 点朝上”的频率为________;
点朝上”的频率为________;
②小红说:“根据实验,出现![]() 点朝上的概率最大.”她的说法正确吗?为什么?
点朝上的概率最大.”她的说法正确吗?为什么?
![]() 小颖和小红在实验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.
小颖和小红在实验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表或画树状图的方法加以说明,并求出其最大概率.