题目内容
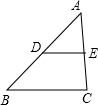
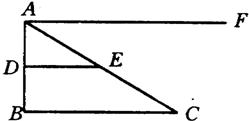 23、如图,DE是△ABC的中位线,∠B=90°,AF∥BC.在射线AF上是否存在点M,使△MEC与△ADE相似?若存在,请先确定点M,再证明这两个三角形相似;若不存在,请说明理由.
23、如图,DE是△ABC的中位线,∠B=90°,AF∥BC.在射线AF上是否存在点M,使△MEC与△ADE相似?若存在,请先确定点M,再证明这两个三角形相似;若不存在,请说明理由.分析:△ADE中,∠ADE=90°,DE是△ABC的中位线,则DE∥BC;如果过点E作EM⊥AC于M,则△AEM中有两个角与△ADE中的两个角分别对应相等,根据相似三角形的判定,可知两三角形相似.
解答:解:存在,过点E作AC的垂线,与AF交与一点,即为M点.
连接MC;
∵DE是△ABC的中位线,
∴DE∥BC,AE=EC.
∵ME⊥AC,
∴△AEM≌△CEM.
∴∠MAE=∠MCE.
∵∠B=90°,
∴∠DAM=90°.
∵AF∥BC,
∴AM∥DE.
∴∠MAE=∠AED.
∴∠AED=∠MCE.
∵∠ADE=∠MEC=90°,
∴△MEC∽△ADE.

连接MC;
∵DE是△ABC的中位线,
∴DE∥BC,AE=EC.
∵ME⊥AC,
∴△AEM≌△CEM.
∴∠MAE=∠MCE.
∵∠B=90°,
∴∠DAM=90°.
∵AF∥BC,
∴AM∥DE.
∴∠MAE=∠AED.
∴∠AED=∠MCE.
∵∠ADE=∠MEC=90°,
∴△MEC∽△ADE.
点评:本题主要考查相似三角形的判定、全等三角形的判定和性质等知识.综合性较强,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
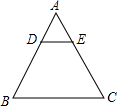 已知:如图,DE是△ABC的中位线,若AD=4,AE=5,BC=12,则△ADE的周长为( )
已知:如图,DE是△ABC的中位线,若AD=4,AE=5,BC=12,则△ADE的周长为( )| A、7.5 | B、15 | C、30 | D、24 |
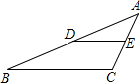 如图,DE是△ABC的中位线,则△ADE和四边形BCED的面积之比为( )
如图,DE是△ABC的中位线,则△ADE和四边形BCED的面积之比为( )| A、1:2 | B、1:3 | C、1:4 | D、以上都不对 |
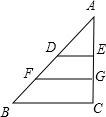 如图,DE是△ABC的中位线,FG是梯形BCED的中位线,若BC=16cm,则FG的长是( )
如图,DE是△ABC的中位线,FG是梯形BCED的中位线,若BC=16cm,则FG的长是( )| A、6 | B、8 | C、10 | D、12 |
 如图,DE是△ABC的中位线,若BC=6,则DE=
如图,DE是△ABC的中位线,若BC=6,则DE= 16、已知:如图,DE是△ABC的中位线,点P是DE的中点,CP的延长线交AB于点Q,那么S△DPQ:S△ABC=
16、已知:如图,DE是△ABC的中位线,点P是DE的中点,CP的延长线交AB于点Q,那么S△DPQ:S△ABC=