题目内容
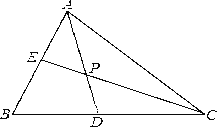
【题目】如图,在等边△BCD中,DF⊥BC于点F,点A为直线DF上一动点,以B为旋转中心,把BA顺时针方向旋转60°至BE,连接EC.
(1)当点A在线段DF的延长线上时,
①求证:DA=CE;
②判断∠DEC和∠EDC的数量关系,并说明理由;
(2)当∠DEC=45°时,连接AC,求∠BAC的度数.

【答案】(1)①证明见解析②∠DEC+∠EDC=90°;(2)150°或30°
【解析】试题分析: ![]() ①证明△BAD≌△BEC,即可证明.
①证明△BAD≌△BEC,即可证明.
②分别求出![]() 和
和![]() 的度数,即可求出∠DEC和∠EDC的数量关系.
的度数,即可求出∠DEC和∠EDC的数量关系.
![]() 分三种情况进行讨论.
分三种情况进行讨论.
试题解析:
(1)①证明:∵把BA顺时针方向旋转60°至BE,
∴![]() 60°,
60°,

![]() 在等边△BCD中,
在等边△BCD中,
![]() ,
, ![]()
![]() ,
,
![]() ,
,
![]() ,
,
∴△BAD≌△BEC,
∴DA=CE;
②判断:∠DEC+∠EDC=90°.
![]() ,
, ![]() ,
, ![]() ,
,
∵△BAD≌△BEC,
∴∠BCE=∠BDA=30°,
![]() 在等边△BCD中,∠BCD=60°,
在等边△BCD中,∠BCD=60°,
∴∠DCE=∠BCE+∠BCD=90°,∴∠DEC+∠EDC=90°.
(2)分三种情况考虑:
①当点A在线段DF的延长线上时(如图1),
由(1)可得, ![]() 是直角三角形,
是直角三角形, ![]() ,
,
当![]() 时,
时,
![]() ,
,
![]() ,
, ![]() ,
,
由(1)得DA=CE,∴CD=DA,在等边![]() 中,
中, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
![]() .
.
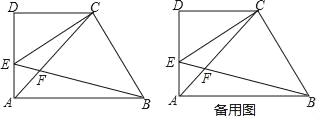
②当点A在线段DF上时(如图2),
以B为旋转中心,把BA顺时针旋转![]() 至BE.
至BE.
![]() ,
,

在等边![]() 中,
中, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
在![]()
![]() ,
,
![]() <
<![]() ,
,
∵DA<DF,DA=CE,
∴CE<DC,
由②可知![]() 为直角三角形,
为直角三角形,
∴∠DEC≠45°.
③当点A在线段FD的延长线上时(如图3),

同第②种情况可得![]() ≌
≌![]() ,
,
![]() ,
,
在等边![]() 中,
中, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,
![]() ,
,
![]() ,
,
![]() ,
,
∴AD=CD=BD,
∵![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
综上所述, 的度数是
![]() 或
或![]()

【题目】小亮与小明做投骰子(质地均匀的正方体)的实验与游戏.
(1)在实验中他们共做了50次试验,试验结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 10 | 9 | 6 | 9 | 8 | 8 |
填空:此次实验中,“1点朝上”的频率是 ;
② 小亮说:“根据试验,出现1点朝上的概率最大.”他的说法正确吗?为什么?
(2)小明也做了大量的同一试验,并统计了“1点朝上”的次数,获得的数据如下表:
试验总次数 | 100 | 200 | 500 | 1000 | 2000 | 5000 | 10000 |
1点朝上的次数 | 18 | 34 | 82 | 168 | 330 | 835 | 1660 |
1点朝上的频率 | 0.180 | 0.170 | 0.164 | 0.168 | 0.165 | 0.167 | 0.166 |
“1点朝上”的概率的估计值是 .