题目内容
 如图,小正方形的边长均为1,线段AE交圆于点B,点A、C、D、E均为小正方形的顶点,则tan∠BCD=
如图,小正方形的边长均为1,线段AE交圆于点B,点A、C、D、E均为小正方形的顶点,则tan∠BCD=| 2 |
| 5 |
| 2 |
| 5 |
分析:由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠BCD=∠BAD,又由在Rt△AEF中,tan∠EAF=
=
,继而求得答案.
| EF |
| AF |
| 2 |
| 5 |
解答: 解:∵∠BAD与∠BCD是
解:∵∠BAD与∠BCD是
所对的圆周角,
∴∠BCD=∠BAD,
在Rt△AEF中,EF=2,AF=5,
∴tan∠EAF=
=
,
∴tan∠BCD=
.
故答案为:
.
 解:∵∠BAD与∠BCD是
解:∵∠BAD与∠BCD是 |
| BD |
∴∠BCD=∠BAD,
在Rt△AEF中,EF=2,AF=5,
∴tan∠EAF=
| EF |
| AF |
| 2 |
| 5 |
∴tan∠BCD=
| 2 |
| 5 |
故答案为:
| 2 |
| 5 |
点评:此题考查了圆周角定理以及正切函数的定义.此题难度不大,注意求一个锐角的三角函数值一般要将这个锐角转化到直角三角形中是解此题的关键.

练习册系列答案
相关题目
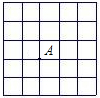 如图,小正方形的边长为1,若以A为顶点的等腰直角三角形的面积为
如图,小正方形的边长为1,若以A为顶点的等腰直角三角形的面积为| 5 |
| 2 |
| A、4个 | B、8个 |
| C、12个 | D、16个 |
 如图,小正方形的边长均为1,则下面图中的三角形(阴影部分)与△ABC相似的是( )
如图,小正方形的边长均为1,则下面图中的三角形(阴影部分)与△ABC相似的是( )
 (2012•北塘区二模)如图,小正方形的边长均为1,扇形OAB是某圆锥的侧面展开图,则这个圆锥的底面周长为( )
(2012•北塘区二模)如图,小正方形的边长均为1,扇形OAB是某圆锥的侧面展开图,则这个圆锥的底面周长为( ) 如图,小正方形的边长为1,试在图中作出2条长度不是有理数的线段和两条长度是有理数的线段.
如图,小正方形的边长为1,试在图中作出2条长度不是有理数的线段和两条长度是有理数的线段.