题目内容
把一个矩形剪去一个正方形，所余的矩形与原矩形相似，那么原矩形的长与宽之比为
- A.2：1
- B.
：1 - C.5：2
- D.（1+
）：2
D
分析：根据相似多边形对应边的比相等，对应角相等可知．
解答：
解：在矩形ABDC中截取正方形ABFE，
则矩形ABDC∽矩形FDCE，
则
，
设矩形ABDC的边BD=a，AB=DC=b．
则DF=a-b，
得到：
，
即
，
设
=x，
则得到：x-1=
，
解得：x=（1+）：2，
原矩形的长与宽之比为（1+）：2．
故选D．
点评：本题就是考查相似形的对应边的比相等，分清矩形的对应边是解决本题的关键．
分析：根据相似多边形对应边的比相等，对应角相等可知．
解答：
解：在矩形ABDC中截取正方形ABFE，则矩形ABDC∽矩形FDCE，
则
，设矩形ABDC的边BD=a，AB=DC=b．
则DF=a-b，
得到：
，即
，设
=x，则得到：x-1=
，解得：x=（1+
）：2，原矩形的长与宽之比为（1+
）：2．故选D．
点评：本题就是考查相似形的对应边的比相等，分清矩形的对应边是解决本题的关键．
练习册系列答案
相关题目
略不计，如图2）．设剪去的正方形边长为x（cm），x为正整数．折成的长方体盒子底面积为y（cm2）．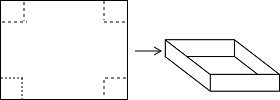
略不计，如图2）．设剪去的正方形边长为x（cm），x为正整数．折成的长方体盒子底面积为y（cm2）．