题目内容
【题目】在
中，点
，
，
依次是边
的四等分点，点
，
，
依次是边
的四等分点，分别以
，
，
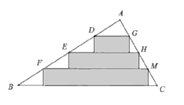
为边向下剪三个宽相等的矩形，如图所示．若图中空白部分的面积和为
，则图中阴影部分的面积和是（ ）
A.
B.
C.
D.
【答案】B
【解析】
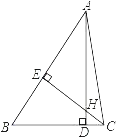
过点A作DG的垂直线AK， 三个宽相等的矩形宽度设为h，利用角角边可证得
，从而得出BQ=FO=EP=DK，NC=SM=RH=KG， AK=DP=EO=FQ=h ，AK=GR=HS=MN=h
因空白部分的面积和为8，所以
得出
，可求得阴影矩形FQNM面积、矩形EOSH面积、矩形DPRG面积，即可求得阴影部分面积=阴影矩形FQNM面积+矩形EOSH面积+矩形DPRG面积．
过点A作DG的垂直线AK， 三个宽相等的矩形宽度设为h
∵点
，
，
依次是边
的四等分点，点
，
，
依次是边
的四等分点
∴AD=DE=EF=FB ，AG=GH=HM=MC，
∵四边形FQNM、四边形EOSH、四边形DPRG为矩形且高相等
∴
，
∴
，
，
∵AD=DE=EF=FB，AG=GH=HM=MC
，，
，
∴，
∴BQ=FO=EP=DK，NC=SM=RH=KG，AK=DP=EO=FQ=h ，AK=GR=HS=MN=h ，
∴
∵图中空白部分的面积和为8
∴
∵BQ=FO=EP=DK，NC=SM=RH=KG
∴阴影矩形FQNM面积为：
=
=
=12
同理，矩形EOSH面积为：
=
=
=8
矩形DPRG面积为：
=
==4
∴阴影部分面积=阴影矩形FQNM面积+矩形EOSH面积+矩形DPRG面积=12+8+4=24
故选：B
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
【题目】某单位需招聘一名技术员，对甲、乙、丙三名候选人进行了笔试和面试两项测试，其成绩如下表所示．根据录用程序，该单位又组织了
名人员对三人进行民主评议，其得票率如扇形图所示，每票
分（没有弃权票。每人只能投票）
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
笔试 |
|
|
|
面试 |
|
|
|
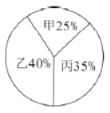
（1）请算出三人的民主评议得分．
（2）该单位将笔试、面试、民主评议三项得分按
确定综合成绩，且民主评议得分低于
分不录取，谁将被录用？请说明理由．
