Question

【题目】如图，在Rt△ABC中，CA=CB=2，M为CA的中点，在AB上存在一点P，连接PC、PM，则△PMC周长的最小值是（ ）

A.
B.
C. +1
D. +1

Answer 1

【答案】C
【解析】解：作点C关于直线AB的对称点D，连接DM交AB于点P，此时△PCM周长最小．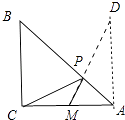

∵CA=CB，∠ACB=90°，
∴∠BAC=∠B=∠BAD=45°，
在RT△ADM中，∵∠DAM=90°，AD=2，AM=1，
∴DM= = ，
∴此时△PCM的周长为PC+PM+CM=PM+PD+CM= +1．
故选C．
【考点精析】利用轴对称-最短路线问题对题目进行判断即可得到答案，需要熟知已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．