题目内容

阅读：D为△ABC中BC边上一点，连接AD，E为AD上一点．
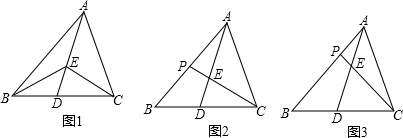
如图1，当D为BC边的中点时，有S_△EBD=S_△ECD，S_△ABE=S_△ACE；
当 $数学公式$ 时，有 $数学公式$ ．
解决问题：
在△ABC中，D为BC边的中点，P为AB边上的任意一点，CP交AD于点E、设△EDC的面积为S₁，△APE的面积为S₂．
（1）如图2，当 $数学公式$ 时， $数学公式$ 的值为；
（2）如图3，当 $数学公式$ 时， $数学公式$ 的值为；
（3）若S_△ABC=24，S₂=2，则 $数学公式$ 的值为______．

解：如图：
（1）连接BE，延长交AC于F．
∵D为BC中点，∴S_△EBD=S_△ECD，S_△ABE=S_△ACE，
∵P为AB上的一点，且 $\text{[math]}$ ，
∴F为AC的中点（三角形三条中线交于一点）．
∴S_△AEP=S_△BEP，S_△AEF=S_△CEF，S_△ABF=S_△CBF，
∵S_△ABF=S_△AEP+S_△BEP+S_△AEF=2S_△AEP+S_△AEF=S_△EBD+S_△ECD+S_△CEF=2S_△ECD+S_△CEF∴S_△AEP=S_△ECD，∴ $\text{[math]}$ =1．

（2）当 $\text{[math]}$ 时，S_△BPE=nS_△APE=nS₂，
S_△BEC=2S₁，S_△AEC=S_△AEB=（n+1）S₂，
由S_△BPC=nS_△APC，得
2S₁+nS₂=n（S₂+S₂+nS₂）
解得： $\text{[math]}$ = $\text{[math]}$ ；

（3）当S_△ABC=24，S₂=2，
由（2）的结论可知， $\text{[math]}$ ，
解得n=2或-5（舍去负值）．
∴ $\text{[math]}$ =2．
分析：（1）由已知得，P为AB的中点，根据三角形三条中线交于一点的性质，对面积进行转化；
（2）由于AD为中线，可知，∴S_△EBD=S_△ECD，S_△ABE=S_△ACE，根据“等高的两个三角形面积比等于底边的比”，列出等式求 $\text{[math]}$ ；
（3）充分运用（2）的结论，已知条件，列方程组求n，即 $\text{[math]}$ 的值．
点评：本题考查了三角形的中线等分面积的性质，等高的两个三角形面积比等于底边的比的性质．