题目内容
提出问题
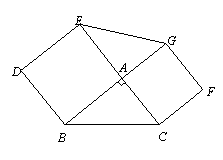
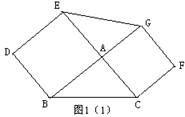
如图,在△ABC中,∠A=90°,分别以边AB、AC向外作正方形ABDE 和正方形 ACFG,连接EG,小亮发现△ABC与△AEG面积相等.小亮思考:这个问题中,如果∠A≠90°,那么△ABC与△AEG面积是否仍然相等?
猜想结论
经过研究,小亮认为:上述问题中,对于任意△ABC,分别以边AB、AC向外作正方形ABDE 和正方形 ACFG,连接EG,那么△ABC与△AEG面积相等.
证明猜想
(1)请你帮助小亮画出图形,并完成证明过程.已知:以△ABC的两边AB、AC为边长分别向外作正方形ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
结论应用
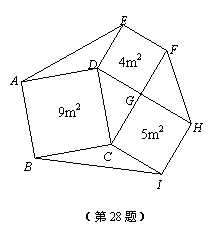
(2)学校教学楼前的一个六边形花圃被分成七个部分,分别种上不同品种的花卉,其中四边形ABCD、CIHG、GFED均为正方形,且面积分别为9m2、5m2和4m2.求这个六边形花圃ABIHFE的面积.
 |
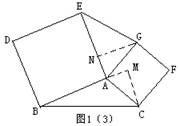
(1)证明:①如图(1),当∠BAC=90°时,
△EAG≌△BAC(SAS),∴S△AEG=S△ABC. ………………2分
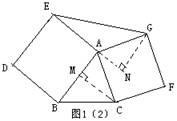
②如图(2),当∠BAC<90°时,过C作CM⊥AB,垂足为M,
过G作GN⊥AE,与AE的延长线交于点N.
∵∠GAN +∠NAC =∠GAC =90°,∠MAC +∠NAC =∠MAN = 90°,
∴∠GAN =∠MAC,又AC =AG,∠AMC =∠ANG =90°.
∴△AMC≌△ANG,∴GN = CM.
又S△AEG=![]() AE·GN,S△ABC=
AE·GN,S△ABC=![]() AB·CM,
AB·CM,
∴S△AEG = S△ABC. ………………5分
③如图(3),当∠BAC>90°时,
如图中辅助线,仿照⑵,同理可证.
综合以上结论可知,命题成立.………………7分
(2)解:∵正方形ABCD、CIHG、GFED的面积分别为9m2、5m2和4m2,
∴DC2=9m2,CG2=5m2,DG2=4m2.
∵DC2=CG2+DG2,∴三角形DCG是直角三角形,∠DGC=90°.
∴S△DCG=![]() ·DG·CG=
·DG·CG=![]() ´2´
´2´![]() =
=![]() m.
m.
∵四边形ABCD、CIHG、GFED均为正方形,
根据上面结论可得:△ADE、△FGH△、△CBI均与△DCG的面积相等,
∴六边形ABIHFE的面积为9+5+4+4´![]() =(18+4
=(18+4![]() ) m2. ……………10
) m2. ……………10

 名校课堂系列答案
名校课堂系列答案
 24、问题背景:某课外学习小组在一次学习研讨中,得到了如下命题:
24、问题背景:某课外学习小组在一次学习研讨中,得到了如下命题: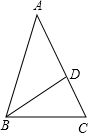 如图,在△ABC中,∠A=36°,AB=AC,BD是∠ABC的平分线,设CD=a,BD=b,AB=c.
如图,在△ABC中,∠A=36°,AB=AC,BD是∠ABC的平分线,设CD=a,BD=b,AB=c.