Question

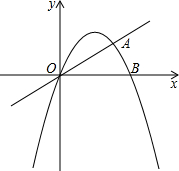已知抛物线y=-x²+

4 3

3

x与x轴交于O点和B点，与直线y=kx在第一象限交于点A（

3

，1）．
（1）求k的值及∠AOB的度数．
（2）现有一个半径为2的动圆，其圆心P在抛物线上运动，当⊙P恰好与y轴相切时，求P点坐标．
（3）在抛物线上是否存在一点M，使得以M为圆心的⊙M恰好与y轴和上述直线y=kx都相切？若存在，求点M的坐标及⊙M的半径；若不存在，请说明理由．

Answer 1

分析：（1）将点A坐标代入直线OA的解析式中即可确定k的值；由点A的坐标，先求出∠AOB的正弦值，由此确定∠AOB的度数．
（2）⊙P与y轴相切时，点P的横坐标的绝对值等于⊙P的半径长，将点P的横坐标代入抛物线的解析式中，即可确定点P的坐标．
（3）⊙M与y轴、直线OA都相切，那么圆心M必为∠AOy的角平分线与抛物线的交点，根据该思路解题即可．

解答：解：（1）将点A（

3

，1）代入直线y=kx中，得：

3

k=1，k=

3

3

；
由A（

3

，1）得：tan∠AOB=

1

3

=

3

3

，则：∠AOB=30°．

（2）∵⊙P恰好与y轴相切，
∴P点到y轴的距离等于⊙P的半径，即 P点的横坐标为 2或-2；
当x=2时，y=-2²+

4 3

3

×2=-4+

8 3

3

；
当x=-2时，y=-（-2）²+

4 3

3

×（-2）=-4-

8 3

3

；
∴P（2，-4+

8 3

3

）或（-2，-4-

8 3

3

）．

（3）∵由（1）知：∠AOB=30°，则∠AOy=60°；
∴∠AOy的角平分线：y=

3

x．
联立抛物线的解析式，得：

y= 3 x y=-x2+ 4 3 3 x

，
解得：

x1=0 y1=0

（舍去），

x2= 3 3 y2=1

，
∴点M的坐标（

3

3

，1），⊙M的半径为

5 3

3

、

3

3

．

点评：考查了二次函数综合题，该题主要考查的是函数图象交点坐标的求法以及直线与圆的位置关系，题目的难度不大，后两问中，能够根据圆与直线相切判断出圆心的位置是解题的关键．