题目内容
如图所示,直线y=﹣ x+
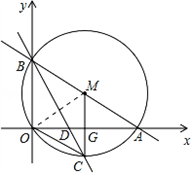
x+ 与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
(1)求证:MC⊥OA;
(2)求直线BC的解析式.
 x+
x+ 与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.(1)求证:MC⊥OA;
(2)求直线BC的解析式.

|
(1)证明:∵∠COD=∠OBC, |
 |

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
题目内容
 x+
x+ 与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
|
(1)证明:∵∠COD=∠OBC, |
 |

 活力课时同步练习册系列答案
活力课时同步练习册系列答案