题目内容
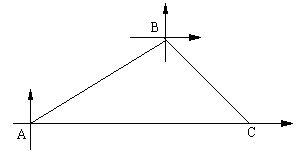
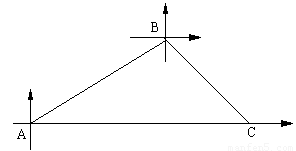
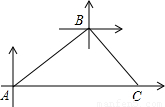
甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会和,于是甲船改变了行进的方向,沿着东南方向航行,结果在小岛C处与乙船相遇、假设乙船的速度和航向保持不变,求:港口A与小岛C之间的距离?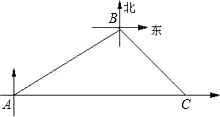
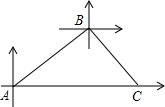
分析:根据题意画出图形,再根据平行线的性质及直角三角形的性质解答.
解答: 解:由题意可知:∠1=60°,∠2=30°,∠4=45°,AB=30海里,
解:由题意可知:∠1=60°,∠2=30°,∠4=45°,AB=30海里,
过B作BD⊥AC于D,则∠1=∠3=60°,
在Rt△BCD中,∵∠4=45°,∴CD=BD,
在Rt△ABD中,∵∠2=30°,AB=30海里,
∴BD=
AB=15海里,AD=•cos30°=30×
=15
海里,
∴AC=AD+CD=15
+15(海里).
故港口A与小岛C之间的距离是(15
+15)海里.
 解:由题意可知:∠1=60°,∠2=30°,∠4=45°,AB=30海里,
解:由题意可知:∠1=60°,∠2=30°,∠4=45°,AB=30海里,过B作BD⊥AC于D,则∠1=∠3=60°,
在Rt△BCD中,∵∠4=45°,∴CD=BD,
在Rt△ABD中,∵∠2=30°,AB=30海里,
∴BD=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴AC=AD+CD=15
| 3 |
故港口A与小岛C之间的距离是(15
| 3 |
点评:此题比较简单,解答此题的关键是过B作BD⊥AC,构造出直角三角形,利用特殊角的三角函数值及直角三角形的性质解答.

练习册系列答案
相关题目
 会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求: