题目内容
匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),这个容器的形状是下图中的( )
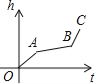
A. 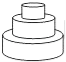 B.
B. 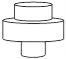 C.
C. 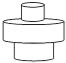 D.
D. 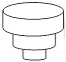
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),这个容器的形状是下图中的( )

A.  B.
B.  C.
C.  D.
D. 
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案