题目内容
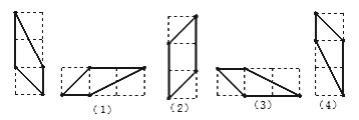
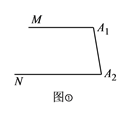
【题目】(1)如图①,![]() ,则
,则![]() _________.
_________.
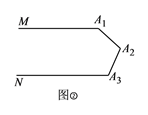
如图②,![]() ,则
,则![]() ___________.
___________.
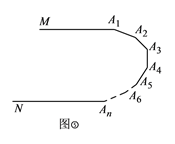
如图③,![]() ,则
,则![]() ___________.
___________.
如图④,![]() ,则
,则![]() ___________.
___________.
从上述结论中你发现了什么规律?请在图②,图③,图④中选一个证明你的结论.


(2)如图⑤,![]() ,则
,则![]() ______________.
______________.
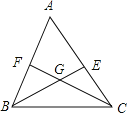
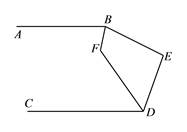
(3)利用上述结论解决问题:如图已知![]() ,
, ![]() 和
和![]() 的平分线相交于
的平分线相交于![]() ,
, ![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)![]() ,
, ![]() ,
, ![]() ,
, ![]() (2)
(2)![]() ;(3)证明见解析.
;(3)证明见解析.
(3)过![]() 点作
点作![]() ,则
,则![]() .
.
则![]() ,又
,又![]() ,得
,得![]() ,故
,故![]() .
.
【解析】试题分析:观察图形①,由MA1∥NA2结合平行线的性质,两直线平行同旁内角互补,即可得到![]() 的值;在图②中,过A2作A2O平行于M A1,连续利用两次“两直线平行同旁内角互补”,即可得到
的值;在图②中,过A2作A2O平行于M A1,连续利用两次“两直线平行同旁内角互补”,即可得到![]() 的值,同理即可解答
的值,同理即可解答![]() 和
和![]() 的值;
的值;
![]() 根据(1)中的结果,观察其中的规律,看它们的角度有什么变化,
根据(1)中的结果,观察其中的规律,看它们的角度有什么变化,
![]() 过
过![]() 点作
点作![]() ,则
,则![]() .根据(1)中的结论以及角平分线的定义,即可得到
.根据(1)中的结论以及角平分线的定义,即可得到![]()
试题解析:
(1)(1)如图①,根据MA1∥NA2,可得![]()
如图②,过![]() 作PA2∥MA1,
作PA2∥MA1,
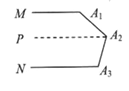
∵MA1∥NA3,
∴PA2∥MA1∥NA3,
![]()
![]()
如图③,过A2作PA2∥MA1,过A3作QA3∥MA1,
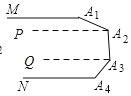
∵MA1∥NA3,
∴QA3∥PA2∥MA1∥NA3,
![]()
![]()
同理可得: ![]()
故答案为: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
(2)根据![]() 可得:
可得: ![]()
(3)过![]() 点作
点作![]() ,则
,则![]() .
.
则![]() ,
,
又![]() ,
,
得![]() ,
,
故![]() .
.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目