题目内容
在平面直角坐标系中,直线 (k为常数且k≠0)分别交x轴、y轴于点A、B,⊙O半径为
(k为常数且k≠0)分别交x轴、y轴于点A、B,⊙O半径为 个单位长度.
个单位长度.⑴如图甲,若点A在x轴正半轴上,点B在y轴正半轴上,且OA=OB.
①求k的值;
②若b=4,点P为直线
 上的动点,过点P作⊙O的切线PC、PD,切点分别为C、D,当PC⊥PD时,求点P的坐标.
上的动点,过点P作⊙O的切线PC、PD,切点分别为C、D,当PC⊥PD时,求点P的坐标.⑵若
 ,直线
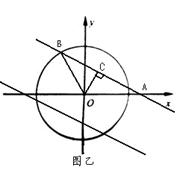
,直线 将圆周分成两段弧长之比为1∶2,求b的值.(图乙供选用)
将圆周分成两段弧长之比为1∶2,求b的值.(图乙供选用)

(1)
①k=-1
②P的坐标为(1,3)或(3,1)
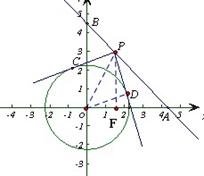
(2)b的值为
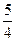 或
或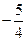 解析:
解析:⑴①根据题意得:B的坐标为(0,b),∴OA=OB=b,
∴A的坐标为(b,0),代入y=kx+b得k=-1.
②过P作x轴的垂线,垂足为F,连结OD.
∵PC、PD是⊙O的两条切线,∠CPD=90°,
∴∠OPD=∠OPC=
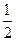 ∠CPD=45°,
∠CPD=45°,∵∠PDO=90°,,∠POD=∠OPD=45°,
∴OD=PD=
 ,OP=
,OP=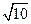 .
.∵P在直线y=-x+4上,
设P(m,-m+4),则OF=m,PF=-m+4,
∵∠PFO=90°, OF2+PF2=PO2,
∴ m2+ (-m+4)2=(
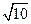 )2,
)2,解得m=1或3,
∴P的坐标为(1,3)或(3,1)
⑵分两种情形,y=-
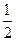 x+
x+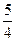 ,或y=-
,或y=-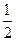 x-
x-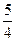 。
。直线
 将圆周分成两段弧长之比为1∶2,可知其所对圆心角为120°,
将圆周分成两段弧长之比为1∶2,可知其所对圆心角为120°,如图,画出弦心距OC,可得弦心距OC=
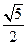 ,
,又∵直线
 中
中 ∴直线与x轴交角的正切值为
∴直线与x轴交角的正切值为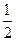 ,即
,即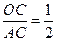 ,∴AC=
,∴AC= ,进而可得AO=
,进而可得AO=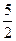 ,即直线与与x轴交于点(
,即直线与与x轴交于点(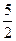 ,0).
,0).所以直线与y轴交于点(
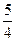 ,0),所以b的值为
,0),所以b的值为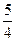 .
.当直线与x轴、y轴的负半轴相交,同理可求得b的值为
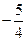 .
.综合以上得:b的值为
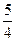 或
或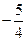 .
.

练习册系列答案
相关题目
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.