Question

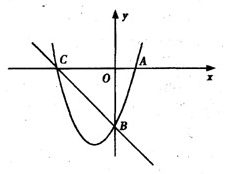
如图，已知抛物线y＝x²+x+2交x轴于A、B两点（点A在点B的左侧），与y轴交于点C.

1.求点A、B、C的坐标.

2.若点M为抛物线的顶点，连接BC、CM、BM，求△BCM的面积

3.连接AC，在x轴上是否存在点P使△ACP为等腰三角形，若存在，请求出点P的坐标；若不存在请说明理由

 

Answer 1

 

1.A（－1,0）、B（5,0）、C（0,2）(2分)

2.6

3.（－1－,0）、（－1，0）、

（，0）

解析:.解：（1）令x²+x+2＝0，解得＝－1,＝5(1分)

令x＝0,则y＝2,所以A、B、C的坐标分别是A（－1,0）、B（5,0）、C（0,2）(2分)

（2）顶点M的坐标是M（2，）(3分)

过M作MN垂直y轴于N,

所以△BCM的面积＝－－

＝(2+5)×－×5×2－×(－2)×2＝6(5分)

（3）当以AC为腰时，在x轴上有两个点分别为,，易求AC＝(6分)

则0＝=1+,O＝－1,

所以,的坐标分别是（－1－,0），（－1，0）(7分)

当以AC为底时，作AC的垂直平分线交x轴于，交y轴于F，垂足为E，

CE＝(8分)

易证△CEF∽△COA所以,而,所以,CF＝

OF＝OC－CF＝2－＝， EF＝(10分)

又△CEF∽△OF，所以，求得O＝

则的坐标为（，0）(11分)

所以存在、、三点，它们的坐标分别是

（－1－,0）、（－1，0）、

（，0）（12分）