题目内容
 等腰梯形ABCD中,AD∥BC,AB=DC,折叠梯形ABCD,使点B与点D重合,EF为折痕,且DF⊥BC,下列结论:①AC=BD;②△BFD为等腰直角三角形;③EF∥AC;④AD+FC=DF
等腰梯形ABCD中,AD∥BC,AB=DC,折叠梯形ABCD,使点B与点D重合,EF为折痕,且DF⊥BC,下列结论:①AC=BD;②△BFD为等腰直角三角形;③EF∥AC;④AD+FC=DF
其中正确的有_____个.
- A.1
- B.2
- C.3
- D.4
D
分析:根据等腰梯形及折叠的性质和等腰直角三角形的性质、全等三角形的判定对各个选项进行分析,然后再进行判断即可.
解答:∵等腰梯形ABCD中,AD∥BC,AB=DC,
∴BD=AC,
故①AC=BD正确;
由折叠的性质知:EF垂直平分BD;
∴EF⊥BD,BF=DF;
又∵DF⊥BF,
∴△BDF是等腰直角三角形;故②正确;
∵ ,
,
∴△DBC≌△ACB(SSS),
∵∠DBF=45°;
∴∠ACB=∠DBC=45°;
∵∠BFD=90°,∠BFO=∠DFO,
∴∠BFO=∠DFO=45°,
∴∠BFO=ACB=45°;
∴EF∥AC;
故③正确;
过A作AG⊥BC,则BG=FC;
∴DF=BF=BG+GF=AD+FC;故④正确;
故正确的有4个,
故选:D.
点评:此题主要考查的是等腰梯形的性质、折叠的性质,两直线平行的判定等知识,熟练利用等腰梯形的性质得出是解题关键.
分析:根据等腰梯形及折叠的性质和等腰直角三角形的性质、全等三角形的判定对各个选项进行分析,然后再进行判断即可.
解答:∵等腰梯形ABCD中,AD∥BC,AB=DC,
∴BD=AC,
故①AC=BD正确;
由折叠的性质知:EF垂直平分BD;
∴EF⊥BD,BF=DF;
又∵DF⊥BF,
∴△BDF是等腰直角三角形;故②正确;

∵
 ,
,∴△DBC≌△ACB(SSS),
∵∠DBF=45°;
∴∠ACB=∠DBC=45°;
∵∠BFD=90°,∠BFO=∠DFO,
∴∠BFO=∠DFO=45°,
∴∠BFO=ACB=45°;
∴EF∥AC;
故③正确;
过A作AG⊥BC,则BG=FC;
∴DF=BF=BG+GF=AD+FC;故④正确;
故正确的有4个,
故选:D.
点评:此题主要考查的是等腰梯形的性质、折叠的性质,两直线平行的判定等知识,熟练利用等腰梯形的性质得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

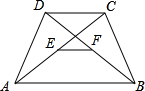 如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积.
如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积. (1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
(1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
 在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,
在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°, 等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是
等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是